Keimbildung und Wachstum bei veränderlichen p und T

Next: Heterogene Keimbildung an Korngrenzen Up: Kinetik druckinduzierter Phasenübergänge Previous: Korngrößen- und Clustergrößenverteilungen

Keimbildung und Wachstum bei veränderlichen p und T

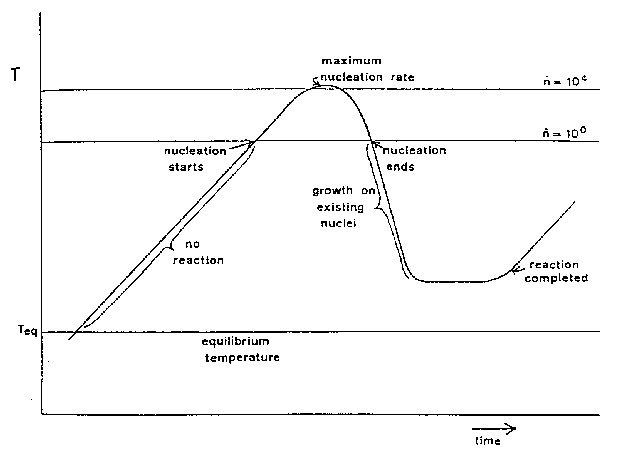
Metamorphe Reaktionen der gesteinsbildenden Minerale treten in der Natur in der Regel in Verbindung mit Uplift- oder Subduktionsvorgängen der Lithosphäre bzw. im Mantel als Resultat der globalen Plattentektonik bzw. Konvektionsströme auf. Die dabei herrschenden thermodynamischen Randbedingungen ändern sich zwar sehr langsam - verglichen mit der Zeitskala von Mineralreaktionen im Labormaßstab - aber doch stetig. Ein typischer Temperatur-Zeit Pfad ist in der folgenden Abbildung dargestellt.

Abb. Schematischer Temperaturverlauf einer endothermen Mineralreaktion beim Abtauchen von lithosphärischem Gestein (prograder Pfad). Nach dem Einsetzen der Keimbildung fällt die Temperatur infolge der verbrauchten latenten Wärme ab, danach setzt die Keimbildung praktisch aus und die Reaktion wird nur durch Wachstum komplettiert
(Abbildung aus (Ridley(1985)), $\dot{n} \sim$ Keimbildungsrate).

Aus diesem Grund ist es notwendig, Keimbildungs- und Wachstumsraten in Abhängigkeit von den jeweiligen p,T-Bedingungen der Gesteine ausdrücken zu können. Für den sehr häufigen Fall des interface-kontrollierten Wachstums und für homogene Keimbildung im Volumen folgen z.B. die Reaktionsraten (siehe (Christian(1975)))

$\begin{displaymath} I^V=I^V_0T \exp\Bigl[-{Q_a+pV_a \over RT}\Bigr] \exp\Bigl[-{\Delta G^*_{hom}\over kT}\Bigr] \quad \quad \hbox{``Keimbildung''}\end{displaymath}$ (36)

und

$\begin{displaymath} Y=Y_0 T \exp\Bigl[-{Q_a+pV_a\over RT}\Bigr] \Bigl\{1-\exp\Bi... ...lta \mu \over RT}\Bigr]\Bigr\} \quad \quad \hbox{``Wachstum''}.\end{displaymath}$ (37)

Die Bedeutung der einzelnen Variablen ist in den im Anhang befindlichen Arbeiten ausführlich erläutert (z.B. in (Daßler et al.(1996))). Zur Bestimmung des Phasenumsatzes gemäß Gleichung (30) müssen die externen p,T-Migrationspfade des Gesteins explizit bestimmt werden, eine Aufgabe in erster Linie für die Geothermie, da der Druck in den meisten Fällen in guter Näherung mit dem lithostatischen Druck übereinstimmt. Für den Fall der subduzierenden Lithosphäre stehen dazu analytische bzw. semi-analytische Lösungen nach McKenzie zur Verfügung ((McKenzie(1969); McKenzie(1970))). Gleichung (30) ist in der Form

$\begin{displaymath} x_{3D}(t) = 1 - \exp \Big\{ - {{4\pi}\over 3} \int\limits_0^... ...bigg( \int\limits_{t_1}^t\!Y(t_2)\,dt_2 \bigg)^3 \,dt_1 \Bigr\}\end{displaymath}$ (38)

bereits früher von (Kirkpatrick(1981)) eingeführt und ausführlich diskutiert worden. Infolge der Feedback-Mechanismen bei Phasenübergängen erster Art (Volumen- bzw. Entropiesprung) werden jedoch nichtlineare Rückkopplungsmechanismen am Phasenübergang spürbar. Beispiele dafür finden sich bei (Spohn et al.(1988)), (Hort et al.(1993)) sowie (Daß-ler und Yuen(1993)). Durch die Wechselwirkung an der Phasenfront kann es zu thermischen und kinetischen Instabilitäten kommen, falls die korrespondierenden Zeitskalen der beteiligten Prozesse in denselben Größenbereich gelangen, eine Beobachtung, die ganz allgemein auch aus der irreversiblen Thermodynamik bekannt ist ((Glansdorff und Prigogine(1971); Haken(1978))).

Die in den Abschnitten 4.1 und 4.2 beschriebenen (Skalen-)Eigenschaften von Keimbildung und Wachstum gelten auf Grund der zeitlichen Veränderung der Reaktionsraten daher nicht streng, aber in sehr guter (lokaler) Näherung, falls die Zeitskalen der thermo-kinetischen Prozesse separiert bleiben. Auf Grund der extrem geringen Wärmeleitfähigkeit der Gesteine ist dies in vielen Anwendungsfällen gegeben.

Next: Heterogene Keimbildung an Korngrenzen Up: Kinetik druckinduzierter Phasenübergänge Previous: Korngrößen- und Clustergrößenverteilungen

Michael Riedel
10/6/1997