Riedel et al. / Grain-size evolution in subducted oceanic ...

4. Rheological structure of subducted slabs

The rheology of olivine is now reasonably well understood, including the effects of temperature, stress and grain size, although some critical issues, such as the effects of pressure and water, still need further investigation (for a review, see [26][27]). In contrast, the rheology of spinel or modified spinel is very poorly constrained. The only experimental data on spinel rheology is that of Vaughan and Coe [1] and Tingle et al. [28] on a germanate analogue. Some preliminary observations are also available for modified spinel [29][30] suggesting higher strength of modified spinel than olivine in the dislocation creep regime (see also [3]). In the absence of direct experimental data on the rheology of (Mg, Fe)₂SiO₄ spinel or modified spinel, we take the admittedly crude approximation that the rheology of spinel or modified spinel is the same as that of the spinel phase of the germanate analogue (Mg₂GeO₄), after the normalization of temperature by the melting temperature (T/T_m) and stress by the shear modulus (/µ).

Considering the strength distribution of oceanic lithosphere at upper mantle P-T conditions, slab deformation is mainly controlled by olivine creep [31][32]. For differential stresses () below 200 MPa the dominant mode of deformation is power-law creep:

where: d/dt is the creep rate; R is the gas constant; Q₁ is the creep activation energy; V₁ is the creep activation volume; and C₁ is a constant. For differential stresses greater than 200 MPa (low-temperature plasticity), the relevant deformation mechanism is glide-controlled creep (Peierls stress controlled dislocation glide, _p):

with _p=8.5 GPa ([32]), the activation energy Q₂, and a constant C₂.

During fast subduction, any deformation of the cold slab interior is probably described by Eq. 11 , where the values of Q₂ and _p have to be modified to account for the effect of pressure. One possibility to include depth- or pressure-dependence into the creep laws is by rescaling the appropriate activation energies with the depth- or pressure-dependent melting temperature of the material (mantle solidus). We adopt here the method of Rubie [2] and rescale the corresponding parameters according to:

where µ and b are the shear modulus and Burgers vector, respectively, at pressure p, and µ₀ and b₀ are the same parameters at 1 atm. The creep law of fine-grained spinel with grain size _sp is estimated using the experimental data on Mg₂GeO₄ spinel [1] according to: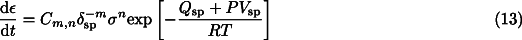

Here, Q_sp and V_sp are the activation energy and activation volume for spinel creep, and C_m,n are suitable constants. We note that this rheological constitutive relation for spinel is not well constrained. For example, for oxide spinel, the dominant deformation mechanism at small grain size is linear diffusion creep rather than non-linear "superplasticity" [33]. Because of this uncertainty, we use three alternative creep laws to model the rheology of spinel: (1) Nabarro-Herring diffusion creep, assuming that diffusion occurs through the lattice (m=2, n=1); (2) Coble diffusion creep, assuming that diffusion occurs predominantly along grain boundaries (m=3, n=1); and (3) structural superplasticity, assuming that grain-boundary sliding is accommodated not by diffusion but by climb of dislocations at grain boundaries (m=2, n=2) [34]. The values of the respective constants C_m,n are chosen to fit Eq. 13 with the experimental data by Vaughan and Coe [1], a method similarly employed in [2].

Table 2. Rheological parameters for olivine and spinel

When the grain-size reduction is not large, then other deformation mechanisms such as the Peierls mechanisms or power-law creep will dominate. The creep strength in these mechanisms is not very different between olivine and spinel [3][28] and we assume that they are identical in this paper. Estimated rheological parameters for olivine and spinel are summarized in Table 2 .

In the two-phase region, we calculate the rheological properties of mixed aggregates of olivine and spinel on the basis of phenomenological flow laws for composite viscous materials. According to this approach [9], the composite creep strength is either given by:

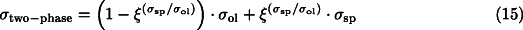
for no grain-size reduction (when spinel forms a "load-bearing framework" within the olivine matrix), or by:

for grain-size reduction during transformation (spinel grains form a "interconnected weak layer" structure, a type of microstructure similar to the one studied theoretically in [6]). Here, is the volume fraction of spinel, and _ol and _sp are the respective creep strengths of the end-member minerals. Eq. 15 has been suggested to describe the composite flow strength of quartz mylonite in quartz-feldspar granitic rock [9], where quartz forms an interconnected matrix of dynamically recrystallized grains that envelop rounded feldspar grains. The deformation stress and strain has been found to be largely partitioned into the fine-grained quartz matrix, whereas, in contrast to quartz, the feldspar grains show few traces of internal strain ([9], p. 290). Here, we argue that a similar situation could arise in the case of a large grain-size reduction resulting from the olivine-spinel phase transformation, so that most of the strain of the slab is partitioned into the relatively weak spinel phase surrounding the olivine host grains.

According to Eq. 15 , a significant reduction in composite flow strength is possible with only a few percent of spinel phase, provided that the contrast in creep strength between both phases is large enough (_sp<<_ol).