





Riedel et al. / Grain-size evolution in subducted oceanic ...
The fundamental physical processes that control grain sizes during and after a first-order phase transformation have been investigated by Riedel and Karato [6]. New grains are formed on grain boundaries in the case of heterogeneous nucleation, growing subsequently at the expense of the host phase. Upon impingement, their size is fixed, which is therefore controlled by the competition between nucleation and growth. Briefly, grain size is small when nucleation dominates over growth, and vice versa.
Theoretical considerations show that the average grain size of the product phase is given approximately by the so-called Avrami length, either in 3D ( Av, grain size after completion of the transformation), or in 2D (
Av, grain size after completion of the transformation), or in 2D (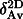 , grain diameter at the formation of continuous films), whereas the half-time of both processes is of the order of the so-called Avrami time (
, grain diameter at the formation of continuous films), whereas the half-time of both processes is of the order of the so-called Avrami time ( Av or
Av or 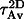 ). These scaling parameters are defined by (see [6]):
). These scaling parameters are defined by (see [6]):
and: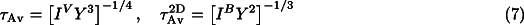
for constant nucleation and growth rates. Here, IV is the nucleation rate per unit volume; that is, the product of the grain-boundary nucleation rate, IB, and the grain-boundary area per unit volume of the reactant phase vOB:
More generally, for time-dependent P-T conditions, Eq. 6 Eq. 7 , calculated at 1% and 99% transition degree, define the range of change of average grain size and transition half-time during the transformation [6]. We shall utilize both scaling laws here: (1) to infer the spinel grain size at or near the formation of continuous films of spinel phase along the olivine grain boundaries ("spinel percolation") on the basis of Eq. 6 , and (2) to estimate the amount of metastable overshoot on the basis of Eq. 7 .
In order to estimate the creep strength of a slab during its subduction, we need to know the spinel grain size at a given point in space,  sp(x, z). For this purpose, we calculate the expected spinel grain size at the beginning of the phase transformation (1st kinetic phase boundary at
sp(x, z). For this purpose, we calculate the expected spinel grain size at the beginning of the phase transformation (1st kinetic phase boundary at  =1%) assuming that it is given by the local value of the Avrami length, Eq. 6 . Afterwards, the spinel grain size changes by two main processes: (1) crystal growth of newly formed spinel grains at the expense of the olivine host phase; and (2) competitive growth of neighbouring "old" spinel grains. In the following, we will make the assumption that the spinel contribution to the composite slab strength in the two-phase region is given by those spinel grains that first formed the continuous films at the beginning of the transformation (process 1). This seems to be justified for cold slabs with a potentially large grain-size reduction, since the dramatic drop in creep strength associated with this reduction would lead to a large viscosity contrast between the stiff matrix of predominantly olivine grains and the weak continuous spinel films percolating through this matrix. The location of this percolation transition is dependent on the extent of grain-size reduction and is therefore kinetically defined. Typically, for a grain-size reduction of 10-100, the percolation transition happens at 10-1% degree of transition [6].Competitive grain growth of fine-grained spinel after site saturation and complete impingement along the olivine grain boundaries (process 2) is likely to occur according to:
=1%) assuming that it is given by the local value of the Avrami length, Eq. 6 . Afterwards, the spinel grain size changes by two main processes: (1) crystal growth of newly formed spinel grains at the expense of the olivine host phase; and (2) competitive growth of neighbouring "old" spinel grains. In the following, we will make the assumption that the spinel contribution to the composite slab strength in the two-phase region is given by those spinel grains that first formed the continuous films at the beginning of the transformation (process 1). This seems to be justified for cold slabs with a potentially large grain-size reduction, since the dramatic drop in creep strength associated with this reduction would lead to a large viscosity contrast between the stiff matrix of predominantly olivine grains and the weak continuous spinel films percolating through this matrix. The location of this percolation transition is dependent on the extent of grain-size reduction and is therefore kinetically defined. Typically, for a grain-size reduction of 10-100, the percolation transition happens at 10-1% degree of transition [6].Competitive grain growth of fine-grained spinel after site saturation and complete impingement along the olivine grain boundaries (process 2) is likely to occur according to: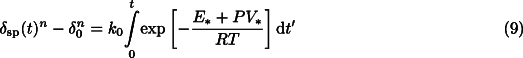
where E* and V* are activation energy and activation volume for spinel grain growth, respectively, and  0 is the grain size at
0 is the grain size at  =1% given by Eq. 6 .
=1% given by Eq. 6 .
Since there are no detailed experimental data available on the grain-growth kinetics in  - or
- or  -spinel of Mg2SiO4, we refrain here from a quantitative modelling of this process. Qualitatively, it is intuitively clear that according to Eq. 9 spinel grain growth will be very sensitive to slab temperature, and small grain size will last only to greater depth when temperatures are low; for example, in the interior of fast subducting slabs.
-spinel of Mg2SiO4, we refrain here from a quantitative modelling of this process. Qualitatively, it is intuitively clear that according to Eq. 9 spinel grain growth will be very sensitive to slab temperature, and small grain size will last only to greater depth when temperatures are low; for example, in the interior of fast subducting slabs.
Within the framework of the present model, the grain size of newly formed spinel will become very large when transformation and subsequent grain growth occur at high temperatures. These very large spinel grain sizes are not realistic, since the growing spinel grains will collide with other minerals, such as pyroxenes or garnets, when the size of newly formed grains exceeds the average size of the starting materials (~3 mm; see, e.g., [25]). At this point growth will stop and the present model will not work. Therefore, in the following we set an upper limit of 3 mm for the spinel grain size.
 (8494 bytes)
(8494 bytes)
Fig. 3. Grain-size reduction accompanying the olivine->spinel transformation and subsequent grain growth in the coldest portion of downgoing slabs. The P-T paths and the labelling as in Fig. 2 . Spinel grain growth (not included in the model) would increase again the grain size at greater depth depending on the P-T conditions.
The resulting grain-size development of spinel with depth for the different P-T paths of Fig. 2 is plotted in Fig. 3 . As it can be seen, a grain-size reduction of up to 4-5 orders of magnitude is possible for slab temperatures below 900 K. The physical reason for this dramatic drop in grain size is the large metastable overshoot,  µ, present at these low temperatures, which leads to a significant change in the balance between nucleation and growth, see discussion.
µ, present at these low temperatures, which leads to a significant change in the balance between nucleation and growth, see discussion.
Copyright © 1997 Elsevier Science B.V., Amsterdam. All Rights Reserved.






 Av, grain size after completion of the transformation), or in 2D (
Av, grain size after completion of the transformation), or in 2D (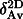 , grain diameter at the formation of continuous films), whereas the half-time of both processes is of the order of the so-called Avrami time (
, grain diameter at the formation of continuous films), whereas the half-time of both processes is of the order of the so-called Avrami time ( Av or
Av or 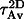 ). These scaling parameters are defined by (see [6]):
). These scaling parameters are defined by (see [6]):
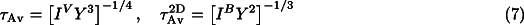







 =1%) assuming that it is given by the local value of the Avrami length,
=1%) assuming that it is given by the local value of the Avrami length, 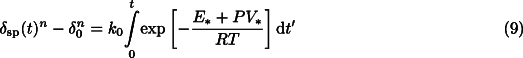
 - or
- or  -spinel of Mg2SiO4, we refrain here from a quantitative modelling of this process. Qualitatively, it is intuitively clear that according to
-spinel of Mg2SiO4, we refrain here from a quantitative modelling of this process. Qualitatively, it is intuitively clear that according to 
 µ, present at these low temperatures, which leads to a significant change in the balance between nucleation and growth, see discussion.
µ, present at these low temperatures, which leads to a significant change in the balance between nucleation and growth, see discussion.