 (32681 bytes)
(32681 bytes)





The thermal structure of subducting slabs depends primarily on the rate of subduction and on the age of the subducting oceanic lithosphere and therefore varies greatly for different subduction zones (see, e.g., [13][14]). Minimum predicted slab temperatures can be as low as 500°C at a depth where the olivine-spinel transition sets in in rapidly subducting slabs of old lithosphere. In younger slabs which subduct at relatively low velocity, the minimum temperature at this depth is likely to be much higher than 500°C. The difference between the P-T conditions inside the slab and those outside is one reason that the slab differs in mineralogy from the equilibrium mantle assemblages outside. The conventional picture of the cold slab implies, in addition, that it should also be mechanically stronger than its surrounding, and thus able to sustain and transmit higher stresses to greater depth (therefore acting as a "stress guide").
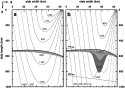
Fig. 1. Slab geometry used for the numerical model. The slab is considered as a rigid body with thickness L and a fixed length of 1000 km. The penetration angle is 45° (upper surface of the slab at the right side). Isotherms (in Kelvin) are calculated using McKenzie's model [11][12], corrected with the latent heat feedback. The bold line shows the phase equilibrium boundary of olivine and-spinel, according to the thermodynamic data of Akaogi et al. [44] Table 1 . (a) vslab=4 cm/yr, L=85 km, Re=59.30. (b) vslab=10 cm/yr, L=85 km, Re=148.25. The metastability region of pure olivine (grey) and the region with mixed olivine-spinel aggregates (dark grey) are shown.
A simple analytical model for the thermal profile of subduction zones is given by McKenzie's solution [11][12] for a slab of finite thickness L subducting into a hotter isothermal mantle of temperature, T0, with constant velocity vslab: 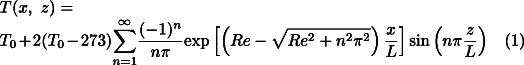
 CpvslabL/2
CpvslabL/2 is the thermal Reynolds number;
is the thermal Reynolds number;  is the density; Cp is the specific heat;
is the density; Cp is the specific heat;  is the thermal conductivity of the slab material; and the coordinates (x, z) are parallel to the slab width and length, respectively (Fig. 1 ). According to Eq. 1 , isotherms within the slab are advected downward such that the maximum depth, zmax, reached by any isotherm is proportional to the product of the vertical descent rate (trench-normal convergence rate times the sine of the dip) and the square of plate thickness, zmax~vslab.L2.
is the thermal conductivity of the slab material; and the coordinates (x, z) are parallel to the slab width and length, respectively (Fig. 1 ). According to Eq. 1 , isotherms within the slab are advected downward such that the maximum depth, zmax, reached by any isotherm is proportional to the product of the vertical descent rate (trench-normal convergence rate times the sine of the dip) and the square of plate thickness, zmax~vslab.L2.
The main portion of subducted slabs has an olivine-rich mineralogy in the upper mantle. To simplify the analysis, we assume that a subducting slab is composed of 60% olivine and that this component transforms directly into the spinel phase at a certain depth. At low temperatures, where the transformation of olivine close to the equilibrium pressure is kinetically inhibited, direct transformation to either  - or
- or  -(Mg, Fe)2SiO4 is likely to occur without any change in composition and therefore without long-range diffusion processes [10]. The growth rate of
-(Mg, Fe)2SiO4 is likely to occur without any change in composition and therefore without long-range diffusion processes [10]. The growth rate of  or
or  in this case may be described by a kinetic equation of the form:
in this case may be described by a kinetic equation of the form: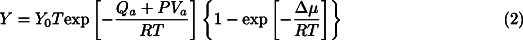
 µ is the molar free energy difference between olivine and spinel; and Y0 is a constant.
µ is the molar free energy difference between olivine and spinel; and Y0 is a constant.
It has been shown that the  ->
-> and
and  ->
-> transition under low (mantle-like) differential stresses of less than about 1 GPa evolves predominantly as a grain-boundary nucleated process; that is, spinel grains nucleate along pre-existing olivine grain boundaries and grow afterwards at the expense of the host olivine [15][16][17]. The appropriate kinetic rate equation for this type of nucleation (compare, e.g., [18]) is:
transition under low (mantle-like) differential stresses of less than about 1 GPa evolves predominantly as a grain-boundary nucleated process; that is, spinel grains nucleate along pre-existing olivine grain boundaries and grow afterwards at the expense of the host olivine [15][16][17]. The appropriate kinetic rate equation for this type of nucleation (compare, e.g., [18]) is: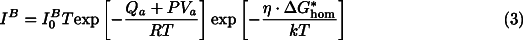
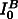 is a pre-exponential constant; k is the Boltzmann constant;
is a pre-exponential constant; k is the Boltzmann constant; 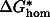 is the activation energy for the formation of a critical nucleus that depends on the thermodynamic driving force
is the activation energy for the formation of a critical nucleus that depends on the thermodynamic driving force  µ; and
µ; and  is the shape factor accounting for the lowering of
is the shape factor accounting for the lowering of 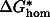 , due to the nucleation at pre-existing grain boundaries (see, e.g., [10][19]).
, due to the nucleation at pre-existing grain boundaries (see, e.g., [10][19]).
The overall transformation kinetics; that is, the volume fraction of the new phase as a function of time,  (t), depend on the rates of both nucleation and growth and are affected by the impingement of the growing grains.
(t), depend on the rates of both nucleation and growth and are affected by the impingement of the growing grains.  (t) is given by [10][18][20]:
(t) is given by [10][18][20]: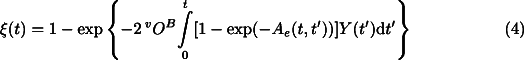
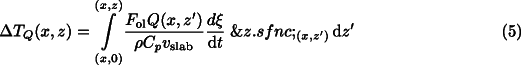
 /dt is the increase in transformation degree at depth (x, z') [10][19][21].
/dt is the increase in transformation degree at depth (x, z') [10][19][21].
In order to obtain the transformed volume fraction of spinel  (t), Eq. 4 , we solve the ordinary differential equations given in Appendix A , Eq. A4 or Eq. A5 , using a 4th-order Runge-Kutta algorithm [22] along a layer of subducting lithosphere for the local P-T conditions. The effect of latent heat, Eq. 5 , is added as a correction term to T(x, z>z') at each integration step z'->z'+dz' within the slab. We neglect the thermal dissipation of the latent heat in the slab, since it is slow compared with the transformation kinetics for fast subduction [23] and would lead only to minor corrections of the McKenzie temperature profile (adiabatic heating included). Typically, the equations are integrated along the direction of subduction z within 10000 steps; that is, for a slab of 1000 km length the integration step width is 100 m.
(t), Eq. 4 , we solve the ordinary differential equations given in Appendix A , Eq. A4 or Eq. A5 , using a 4th-order Runge-Kutta algorithm [22] along a layer of subducting lithosphere for the local P-T conditions. The effect of latent heat, Eq. 5 , is added as a correction term to T(x, z>z') at each integration step z'->z'+dz' within the slab. We neglect the thermal dissipation of the latent heat in the slab, since it is slow compared with the transformation kinetics for fast subduction [23] and would lead only to minor corrections of the McKenzie temperature profile (adiabatic heating included). Typically, the equations are integrated along the direction of subduction z within 10000 steps; that is, for a slab of 1000 km length the integration step width is 100 m.
Table 1. Thermo-mechanical slab constants and kinetic parameters
Table 1 contains a compilation of the thermodynamic parameters used for the thermo-kinetic model. Note that the kinetic parameter for the non-equilibrium transition of  -Mg2SiO4 to
-Mg2SiO4 to  -phase is still subject to large uncertainties (for respective reviews, see [10][24]).
-phase is still subject to large uncertainties (for respective reviews, see [10][24]).
Fig. 2. P-T phase diagram showing the kinetic phase boundaries for 1% and 99% transformation degree (dashed lines). The thick line shows the phase equilibrium of olivine and-spinel, according to the thermodynamic data of Akaogi et al. [44]. The adiabats a-e represent the P-T paths of the coldest portion of a slab (vslab=10 cm/yr) with different thicknesses: (a) L=100 km; (b) L=90 km; (c) L=80 km; (d) L=70 km; (e) L=60 km; (f) boundary condition of the McKenzie model.
The resulting kinetic phase boundaries (1% and 99% transition degree) are shown in Fig. 1 . It can be seen that the thermal structure of a slab is significantly modified by the phase transformation. The non-equilibrium phase boundary of olivine and  -spinel is advected to greater depth (boundary between the region with metastable olivine (grey) and the two-phase region (dark grey)), and the slab temperature is typically increased by 30-130°C. The P-T paths along the central (coldest) portions of slabs with increasing thicknesses are plotted in Fig. 2 . As emphasized previously [10], the latent heat production causes the transformation to occur by a runaway process, which results in steep thermal gradients around the metastable olivine wedge below 600 km depth [19].
-spinel is advected to greater depth (boundary between the region with metastable olivine (grey) and the two-phase region (dark grey)), and the slab temperature is typically increased by 30-130°C. The P-T paths along the central (coldest) portions of slabs with increasing thicknesses are plotted in Fig. 2 . As emphasized previously [10], the latent heat production causes the transformation to occur by a runaway process, which results in steep thermal gradients around the metastable olivine wedge below 600 km depth [19].





