





Riedel et al. / Grain-size evolution in subducted oceanic ...
The most significant result of this paper is the demonstration that a large grain-size reduction can be associated with the olivine to spinel transformation when the transformation occurs at relatively low temperatures but not at high temperatures. The degree of grain-size reduction predicted by the present model for relatively cold slabs (T 900 K) is very large (down to less than 1 µm) and one expects a significant reduction in creep strength in these cases. Before we discuss potential implications, it is appropriate to interpret our results and compare them with some laboratory observations.
900 K) is very large (down to less than 1 µm) and one expects a significant reduction in creep strength in these cases. Before we discuss potential implications, it is appropriate to interpret our results and compare them with some laboratory observations.
 (19560 bytes)
(19560 bytes)
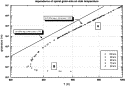
Fig. 4. Arrhenius plot of spinel grain size (logarithmic scale) vs. temperature (reciprocal scale), both numerically determined at the first kinetic phase boundary ( =1%) for different slab thicknesses. The symbols show the values obtained of spinel grain size at
=1%) for different slab thicknesses. The symbols show the values obtained of spinel grain size at  =1% for different subducting layers of lithosphere across the slab. Above 900 K, they follow an Arrhenius dependence with an apparent "activation energy" of about 412 kJ/mol (branch A). Shown as a thick solid line is the semi-analytical solution of Eq. A6 , predicting a slightly higher value of 447 kJ/mol. Note that, within the metastable wedge, the apparent "activation energy" for spinel grain size can be negative (branch B). Predicted grain sizes exceeding ~3 mm are not realistic since the presence of secondary phases such as pyroxenes and garnets prevents the formation of larger spinel grains.
=1% for different subducting layers of lithosphere across the slab. Above 900 K, they follow an Arrhenius dependence with an apparent "activation energy" of about 412 kJ/mol (branch A). Shown as a thick solid line is the semi-analytical solution of Eq. A6 , predicting a slightly higher value of 447 kJ/mol. Note that, within the metastable wedge, the apparent "activation energy" for spinel grain size can be negative (branch B). Predicted grain sizes exceeding ~3 mm are not realistic since the presence of secondary phases such as pyroxenes and garnets prevents the formation of larger spinel grains.
The numerically calculated spinel grain sizes  0 at
0 at  =1% (near the percolation threshold) are plotted as a function of temperature in Fig. 4 . The results include slabs with different initial temperature distributions (variable thicknesses) and different subduction velocities. They show that the dependence of spinel grain size on slab temperature consists of two different branches, in close relationship to the existence of two branches of the kinetic phase boundary shown in Fig. 2 . At high temperatures (branch A), spinel grain size depends on temperature as
=1% (near the percolation threshold) are plotted as a function of temperature in Fig. 4 . The results include slabs with different initial temperature distributions (variable thicknesses) and different subduction velocities. They show that the dependence of spinel grain size on slab temperature consists of two different branches, in close relationship to the existence of two branches of the kinetic phase boundary shown in Fig. 2 . At high temperatures (branch A), spinel grain size depends on temperature as  0~exp(-E*/RT), whereas in cold portions of slabs (branch B), a more complicated behaviour is found: At lower temperatures, the logarithmic plot of grain size vs. T has a negative slope; that is, grain size can decrease with temperature in a certain range.
0~exp(-E*/RT), whereas in cold portions of slabs (branch B), a more complicated behaviour is found: At lower temperatures, the logarithmic plot of grain size vs. T has a negative slope; that is, grain size can decrease with temperature in a certain range.
To interpret this observation and to compare the results with laboratory experiments, we rewrite Eq. 6 as:
Now, within the high temperature branch of the kinetic phase boundary (branch A), the transformation occurs near to equilibrium and the distance between kinetic and equilibrium phase boundary depends only weakly on temperature. The main effect of temperature on grain size comes from the growth rate term (Y) and hence:
Eq. 17 has an Arrhenius type temperature dependence with an apparent "activation energy" similar to that of growth kinetics, in accordance with the numerical results shown in Fig. 4 .
Within the low temperature branch (branch B), the transformation occurs only at a significant overstepping over equilibrium. The amount of metastable overshoot,  P, necessary to start the transformation kinetics can be estimated on the basis of a time scale argument [6][35]: The transformation time scale,
P, necessary to start the transformation kinetics can be estimated on the basis of a time scale argument [6][35]: The transformation time scale,  Av, must be of the order of the time required to pass the overshoot:
Av, must be of the order of the time required to pass the overshoot:
Together with the nucleation and growth rates according to Eq. 2 and Eq. 3 , Eq. 18 defines an implicit relationship for the kinetic phase boundary Pkin(T) ( P
P metastable overshoot, Pkin-Peq) in dependence of temperature, T, which can be solved numerically (a detailed analysis is given in Appendix A ).
metastable overshoot, Pkin-Peq) in dependence of temperature, T, which can be solved numerically (a detailed analysis is given in Appendix A ).
 (17826 bytes)
(17826 bytes)
Fig. 5. Calculated metastable overshoot  P=Pkin-Peq of olivine over the equilibrium pressure with
P=Pkin-Peq of olivine over the equilibrium pressure with  -Mg2SiO4 (Eq. A6 ) under subduction zone conditions (dashed line). The squares show the numerically calculated onset of transformation at
-Mg2SiO4 (Eq. A6 ) under subduction zone conditions (dashed line). The squares show the numerically calculated onset of transformation at  =1% for a slab with thickness L=100 km (integration of the differential Eq. A4 Eq. A5 , thick line=phase equilibrium). For comparison, the isochron
=1% for a slab with thickness L=100 km (integration of the differential Eq. A4 Eq. A5 , thick line=phase equilibrium). For comparison, the isochron  Av=1 h is included, showing the expected location of the kinetic phase boundary at the laboratory time scale (dash-dotted curve). At the geological time-scale, wedge formation sets in at temperatures below 850 K. A compilation of some spinel grain sizes at selected P-T conditions (crosses) is given in Table 3 ; solid diamonds mark the reported P-T conditions of three different high pressure experiments: (1) P=15 GPa, T=1173 K [36], spinel grain size
Av=1 h is included, showing the expected location of the kinetic phase boundary at the laboratory time scale (dash-dotted curve). At the geological time-scale, wedge formation sets in at temperatures below 850 K. A compilation of some spinel grain sizes at selected P-T conditions (crosses) is given in Table 3 ; solid diamonds mark the reported P-T conditions of three different high pressure experiments: (1) P=15 GPa, T=1173 K [36], spinel grain size 1 µm, Eq. 6 predicts 1.8 µm; (2) P=15.5 GPa, T=1273 K [16], spinel grain size
1 µm, Eq. 6 predicts 1.8 µm; (2) P=15.5 GPa, T=1273 K [16], spinel grain size 1.8 µm, Eq. 6 predicts 0.4 µm, (3) P=15.5 GPa, T=1473 K [46], spinel grain size not mentioned, Eq. 6 predicts 4.6 µm.
1.8 µm, Eq. 6 predicts 0.4 µm, (3) P=15.5 GPa, T=1473 K [46], spinel grain size not mentioned, Eq. 6 predicts 4.6 µm.
We find the solution obtained,  P(T), on the basis of Eq. 18 in good agreement with the numerical result of the Runge-Kutta integration of the kinetic differential equations, where we calculate
P(T), on the basis of Eq. 18 in good agreement with the numerical result of the Runge-Kutta integration of the kinetic differential equations, where we calculate  P(T) under the assumption that Pkin is given by the pressure value at 1% transition degree. Both calculation schemes show that metastable hindrance can cause an overshoot of up to 200 km and more at temperatures below 850 K, see Fig. 5 . Typically,
P(T) under the assumption that Pkin is given by the pressure value at 1% transition degree. Both calculation schemes show that metastable hindrance can cause an overshoot of up to 200 km and more at temperatures below 850 K, see Fig. 5 . Typically,  P ranges between 0.7 and 0.4 GPa at temperatures between 950 and 1300 K. Below 900 K, the persistence of metastable olivine to greater depth leads to a different T dependence. Analytically, it follows from Eq. 6 at
P ranges between 0.7 and 0.4 GPa at temperatures between 950 and 1300 K. Below 900 K, the persistence of metastable olivine to greater depth leads to a different T dependence. Analytically, it follows from Eq. 6 at  µ>>RT:
µ>>RT:
with c1=16

 3
3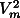 /9k, and
/9k, and  µ(T) is an almost linearly increasing function of T (see Appendix A ). Eq. 19 predicts a minimum grain size of
µ(T) is an almost linearly increasing function of T (see Appendix A ). Eq. 19 predicts a minimum grain size of  0~(I0B/Y0)-1/3 at very large overshoots, whereas at intermediate
0~(I0B/Y0)-1/3 at very large overshoots, whereas at intermediate  µ
µ RT, it predicts a grain size decrease with increasing temperature (branch B of Fig. 4 ).
RT, it predicts a grain size decrease with increasing temperature (branch B of Fig. 4 ).

Table 3. Spinel grain size: comparison with laboratory data
The present results may also be compared with some experimental observations. Rubie and Brearley [36] and Brearley et al. [37] transformed hot pressed forsterite powder to its high-pressure polymorphs by gradually increasing the pressure into the spinel stability field (P=15 GPa) at nearly constant temperatures (T=1173 K) at the laboratory time scale (duration of the experiments 1 h and 5 h, respectively). Their experimental data on grain size of modified spinel phase should therefore be comparable with the here presented grain-size estimations based on the Avrami length taken at these P-T conditions. The results are shown in Fig. 5 and Table 3 . There appears to be a reasonable agreement between the experimental observations and the theoretical estimations, both as to the reachable P-T conditions at the laboratory time-scale as well as to the reported spinel grain sizes. The large difference between laboratory and geologic time scale results hereby in large grain-size differences at the same reference temperature (according to Eq. A9 ), but these differences are, to a great extent, compensated again by the entirely different temperature conditions.
We point out here, however, that the grain-size estimations presented are largely based on the current understanding of the transformation process from olivine to spinel under subduction zone conditions (as reviewed, e.g., in [38][24]). More recent work of Kerschhofer et al. [39] shows that intracrystalline nucleation of spinel may become important at large metastable overshoots of about 18-20 GPa and relatively low temperatures of 1000-1400°C. As of now, since these newly found results are not quantified yet, we state only that an additional shear-induced coherent nucleation mechanism would, of course, affect the above grain size estimations, and that these new findings could be of particular importance for the overall transition kinetics; possible effects could be either a considerable narrowing of the depth of the region of olivine-spinel coexistence or a reduction in the metastable overshoot of olivine in cold slabs.
 (19034 bytes)
(19034 bytes)
Fig. 6. Creep strength of the slab shown in Fig. 1 along its coldest part (slab thickness 85 km) below 400 km. The grain size reduction produces a strength drop of several orders in magnitude, in dependence of the relevant spinel creep mechanism. An average strain rate of 10-15 s-1 is assumed uniformly across the slab.
 (43939 bytes)
(43939 bytes)
Fig. 7. Calculated strength profile of the slab shown in Fig. 1 on the basis of a Nabarro-Herring creep mechanism for spinel (m=2 and n=1 in Eq. 13 ). The creep strength of spinel is assumed to be bounded by the olivine creep strength within the slab. The grey area shows the slab portions with a creep strength higher than 100 MPa; the dark grey shows the slab portions with a creep strength higher than 200 MPa. Note the dramatic strength drop below the tip of the metastable wedge. Spinel grain growth (not included in the model) would cause a significant decrease in the size of the weak zone below the metastable wedge. The two arrows indicate the possible effect of a sustainable pressure drop in the cold interior of fast slabs (see discussion).
The strong dependence of spinel grain size on temperature under the P-T conditions of subducting slabs gives rise to the surprising possibility that the effective viscosity of the slab after the olivine-spinel phase transformation could be higher at higher temperatures (see also the discussion by Rubie and Ross [10], p. 238). In order to investigate this possibility more quantitatively, we plot the creep strength within the slab for a representative strain rate of 10-15 s-1 on the basis of appropriate constitutive equations for olivine and spinel creep in Fig. 6 Fig. 7 .
Fig. 6 shows the creep strength of the slab vs. depth along the coldest portion for three different spinel creep laws and two different subduction velocities. As can be seen, the creep strength in the central portions of fast slabs drops down by several orders of magnitude and assumes a minimum near to the depth where the phase transformation is almost completed (2nd kinetic phase boundary,  =99%). This behaviour appears to be typical for all three grain-size sensitive creep laws (Nabarro-Herring creep, Coble creep and superplasticity, compare Table 2 ). In contrast, the creep strength of a slow slab remains well above these values, suggesting that a warm slab could be (partially) stronger than a cold slab.
=99%). This behaviour appears to be typical for all three grain-size sensitive creep laws (Nabarro-Herring creep, Coble creep and superplasticity, compare Table 2 ). In contrast, the creep strength of a slow slab remains well above these values, suggesting that a warm slab could be (partially) stronger than a cold slab.
In Fig. 7 , we extend this figure into a two-dimensional plot in order to show the rheological structure of a whole slab (Nabarro-Herring creep only). As expected from Fig. 6 , a localized weak zone develops below the tip of the metastable olivine wedge. This weak zone can occupy up to 20% of the slab interior, thus dividing the slab into two comparatively stronger layers at the top and bottom, at depths between 450 and 600 km. In this way it is acting as a kind of low pressure inclusion within the slab body, since the stronger bottom and top layers prevent the undelayed accommodation of the associated density increase by the surrounding hotter mantle. The likely existence of complex internal states of stress produced by the effects of the volume changes accompanying the transformation of peridotite to the transition zone mineral assemblage has also been emphasized recently by Kirby and Okal [40].
Finally, we comment briefly on some geodynamic implications of the present study. It has been argued that deep earthquake activities are related to the transformation of metastable olivine to the modified or spinel phase, since seismicity is high in slabs where metastable olivine is considered to occur [5][38][24][41][42]. Deep earthquakes are hereby believed to occur as a result of the instability of deformation in the ductile regime. The present results provide some insight into the possible mechanisms of deep earthquakes. Combined with the results of thermal models of slabs [19], we propose that the nature of instabilities associated with the olivine-spinel transformation is fundamentally different between the cold and warm branches of the kinetic phase boundary and that instabilities will occur only when the transformation occurs in the cold branch. Our studies suggest two instability mechanisms. One is thermal runaway due to the latent heat release [19]. We have shown that the latent heat release causes positive feedback only when the transformation occurs in the cold branch but not in the hot branch [19], compare also Fig. 2 .
Similarly, the effects of grain-size reduction to cause softening and hence instability will be important only in the cold branch because significant grain-size reduction occurs only at relatively low temperatures. In addition, since the degree of grain-size reduction increases with temperature in this regime (see Fig. 4 and Eq. 19 ), a self-accelerating instability is prone to occur there. Thus, both the effects of latent heat and of grain-size reduction tend to lead to shear instability in the cold branch but not in the hot branch.
Copyright © 1997 Elsevier Science B.V., Amsterdam. All Rights Reserved.






 900 K) is very large (down to less than 1 µm) and one expects a significant reduction in creep strength in these cases. Before we discuss potential implications, it is appropriate to interpret our results and compare them with some laboratory observations.
900 K) is very large (down to less than 1 µm) and one expects a significant reduction in creep strength in these cases. Before we discuss potential implications, it is appropriate to interpret our results and compare them with some laboratory observations.






 =1%) for different slab thicknesses. The symbols show the values obtained of spinel grain size at
=1%) for different slab thicknesses. The symbols show the values obtained of spinel grain size at  0 at
0 at 

 P, necessary to start the transformation kinetics can be estimated on the basis of a time scale argument
P, necessary to start the transformation kinetics can be estimated on the basis of a time scale argument  Av, must be of the order of the time required to pass the overshoot:
Av, must be of the order of the time required to pass the overshoot:
 metastable overshoot, Pkin-Peq) in dependence of temperature, T, which can be solved numerically (a detailed analysis is given in
metastable overshoot, Pkin-Peq) in dependence of temperature, T, which can be solved numerically (a detailed analysis is given in 
 -Mg2SiO4 (Eq. A6 ) under subduction zone conditions (dashed line). The squares show the numerically calculated onset of transformation at
-Mg2SiO4 (Eq. A6 ) under subduction zone conditions (dashed line). The squares show the numerically calculated onset of transformation at  1 µm, Eq. 6 predicts 1.8 µm; (2) P=15.5 GPa, T=1273 K [16], spinel grain size
1 µm, Eq. 6 predicts 1.8 µm; (2) P=15.5 GPa, T=1273 K [16], spinel grain size


 3
3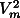 /9k, and
/9k, and  RT, it predicts a grain size decrease with increasing temperature (branch B of
RT, it predicts a grain size decrease with increasing temperature (branch B of 

