Extrapolation kinetischer Phasengrenzen

Die exakte Lokalisierung, in welcher Tiefe die Mineraltransformationen in der subduzierenden Lithosphäre ablaufenden, ist ein Thema von beträchtlichem geodynamischen Interesse ((Rubie(1990))). Prominentes Beispiel dazu ist die Umwandlung von Olivin in Spinell im Bereich der ``transition zone''. Ging man zunächst davon aus, daß sich dieser Übergang in der Nähe des Gleichgewichts beider Phasen vollzieht ((Christensen und Yuen(1984))), so gab es doch seit der Pionierarbeit von (Sung und Burns(1976)) zunehmende Hinweise, daß dies zumindest bei relativ schnell abtauchenden Platten nicht der Fall sein dürfte. Generell zeichnet Phasenübergänge 1. Art aus, daß sie nicht kontinuierlich mit zunehmender Übersättigung beginnen, sondern daß erst eine thermodynamische Aktivitätsbarriere überschritten werden muß, bevor ein signifikanter Phasenumsatz verzeichnet wird.

Die Größe dieses notwendigen metastabilen ``overshoots'' ist abhängig von den Parametern, die in die kinetischen Ratengleichungen von Keimbildung und Wachstum, (36) und (37), eingehen. Diese Parameter sind im Einzelnen (vgl. Diskussion in (Ridley(1985)))

-

Aktivierungsenergie für diffusiven Transport durch das Kristallgitter Q_a:
Typische Werte im Bereich zwischen 150-300 kJ/mol

-

Aktivierungsvolumen für diffusiven Transport V_a (Druckabhängigkeit):
Typische Werte im Bereich zwischen 1-6 cm³/mol

-

Pre-exponentieller Faktor für Keimbildung I^V₀T:
Liegt generell in der Größenordnung Avogadro-Zahl Debye-Frequenz 10⁴⁰ m^-3s^-1

-

Pre-exponentieller Faktor der Wachstumsrate Y₀T:
Muß experimentell für relevanten Wachstumsmechanismus bestimmt werden

-

Oberflächenenergie für Keimbildung:
(Brace und Walsh(1962)) geben einen Bereich von 0.2-2.0 J/m² an. In polykristallinen Gesteinen sind diese Werte nach (Porter und Easterling(1981)) um einen Faktor 3 zu reduzieren

-

Thermodynamische Gleichgewichtseigenschaften (Volumensprung ,
Entropiesprung , Lage der Koexistenzkurve im p,T-Phasendiagramm)

Unter der Voraussetzung, daß diese Größen bekannt sind, ist die Lage der kinetischen Phasengrenze auf der Grundlage des Skalengesetzes (33) bestimmbar:

Die Zeitskala der Phasentransformation muß in derselben Größenordnung liegen wie die Zeit, die zum Überwinden des metastabilen ``overshoots'' notwendig ist, d.h.

 

(43)

Die Geschwindigkeit der Druckänderung ist dabei die Größe, die sich beim Übergang von der Labor- zur geologischen Zeitskala signifikant ändert,

Die Skalenbeziehung (44) wurde für die Umwandlung von Olivin in -Spinell unter den p,T-bedingungen der Subduktionszone von (Riedel und Karato(1996a)) numerisch ausgewertet. Die Forderung der Äquivalenz der Zeitskalen ergibt, kombiniert mit den Reaktionsraten für Keimbildung und Wachstum (36) und (37), eine implizite Gleichung zur Bestimmung von in Abhängigkeit von T,

 

(44)

(die Koeffizienten A_k sind im Anhang von (Riedel und Karato(1996a)) definiert). Die numerische Lösung dieser Gleichung sowohl für die Labor- als auch die geologische Zeitskala zeigt die folgende Abbildung, zusammen mit den p,T-Bedingungen einiger ausgewählter Hochdruckexperimente (vgl. Fig. 5 aus (Riedel und Karato(1996a))):

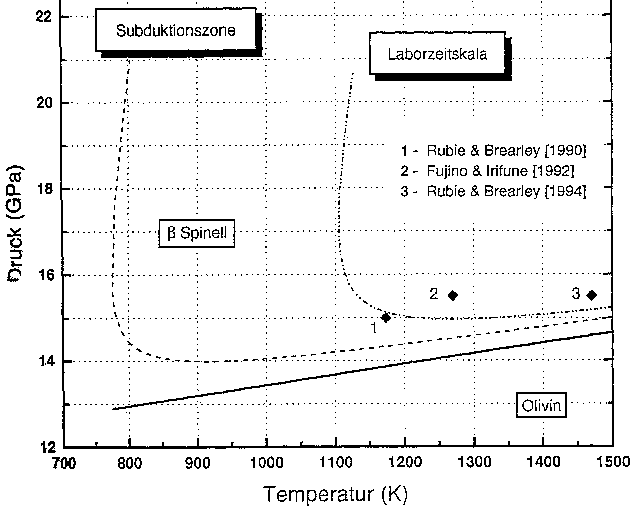
Abb. Kinetische Phasengrenze bei der Umwandlung von Olivin in -Spinell

Kennt man den Verlauf der Phasengrenze auf der Laborzeitskala, so ist es mit Hilfe von Gleichung (44) bzw. (45) möglich, deren Position bei 10^-13 GPa/s zu berechnen, d.h. ihren Verlauf auf die geologische Zeitskala zu extrapolieren ((Riedel(1996))).