Experimentelle Bestimmung der Reaktionsraten

Next: Deformationsexperimente in der Garnet Up: Hochdruckexperimente in der Diamantstempelzelle Previous: Hochdruckmeßplatz für kinetische Experimente

Experimentelle Bestimmung der Reaktionsraten

Ausgangspunkt für die thermodynamische Modellierung der Umsatzkinetik ist Gleichung (30) für die radiale Verteilungsfunktion der sich bildenden Keime der B2-Phase, da sie keine Einschränkungen hinsichtlich der zeitlichen Konstanz von Keimbildung und Wachstum voraussetzt. Auf Grund der gewählten Präparationsmethode (Druckübertragungsmedium Methanol-Äthanol 4:1, enthält geringen Wasseranteil) liegen in nahezu idealer Weise Ausgangsbedingungen für eine homogene Keimbildung vor. Eine mögliche Druckänderung im Probenraum während der Umwandlung wurde über ein lineares Relaxationsgesetz ((Riedel und Daßler(1990a))) im Modell berücksichtigt

$\begin{displaymath} p(t) = p(0) - k_T^{-1} \, C_{KJ}^V \, \delta_{vol} \, x_{3D}(t) \quad ,\end{displaymath}$ (45)

mit $k_T=V^{-1}(\partial V/\partial p)_T$ als isotherme Kompressibilität des Druckübertragungsmediums, C_KJ^V als Volumenanteil der Salzkristalle und $\delta_{vol}=\Delta V/V_{\alpha}$ als relativem Volumensprung bei der Phasenumwandlung. Die Rückkopplung (46) ist Ausdruck der isochoren Randbedingungen, denen generell thermodynamische Zustandsänderungen in geschlossenen Hochdruckzellen unterworfen sind. Berücksichtigt man zusätzlich, daß sich in den häufigsten Anwendungsfällen das mechanische Stützmaterial des Probenraums (Gasket) nicht vollständig starr während des Phasenübergangs verhält, muß der Referenzdruck p(0) noch durch eine zeitabhängige Relaxationsfunktion der Form

$\begin{displaymath} p_{gasket}(t) \sim p(0) \exp[-t/t_0]\end{displaymath}$ (46)

ersetzt werden, die die rheologische Eigenschaften des Gaskets beschreibt ((Riedel und Daßler(1992))). Die Kombination von Gleichung (46) und (47) liefert den einfachsten Fall der Überlagerung zweier zeitabhängiger Prozesse bei strukturellen Phasenübergängen, der Überlagerung des nichtlinearen Druckabfalls infolge der Dichtedifferenz beider Phasen mit der zeitlichen Veränderung der thermodynamischen Randbedingungen infolge des rheologischen Fließens der Umgebung. In dieser Hinsicht besitzt das Problem eine Analogie zu dem Fall des Olivin-Spinell Übergangs in subduzierenden Platten ozeanischer Lithosphäre (siehe nächstes Kapitel).

Mit der Methode der Bildverarbeitung wurde aus den experimentell gemessenen Clustergrößenverteilungen der B2-Phase Rückschlüsse auf den Wachstumsmechanismus gezogen ((Daßler und Riedel(1991b); Riedel und Daßler(1992))).

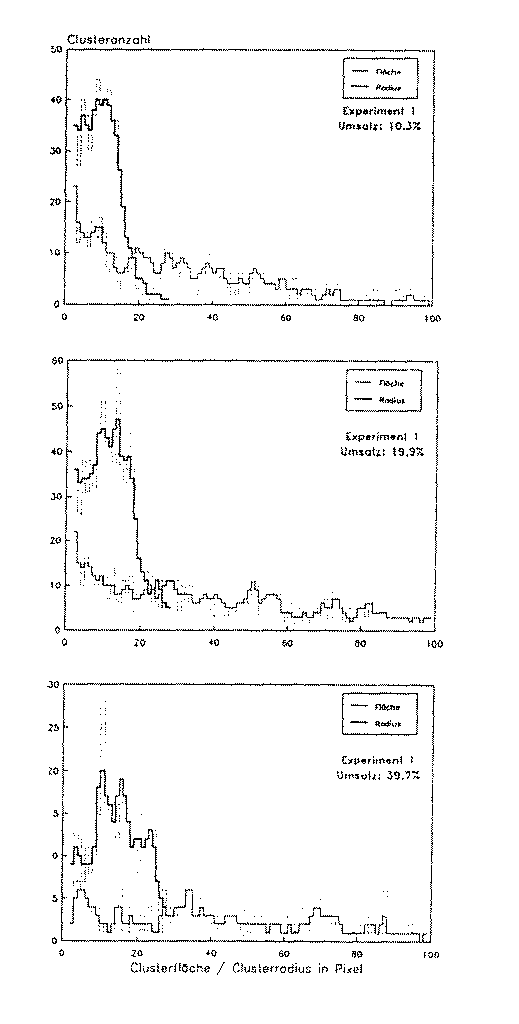
Abb. 2: Mikrostrukturevolution (Clustergrößenverteilung) in der Diamantstempelzelle ((Riedel und Däßler(1992)))

Für das Kristallwachstum (aus einer wässrigen Lösung) existieren im allgemeinen zwei Grenzfälle, je nachdem, welcher Ratenprozeß beim Wachstum zeitlich limitierend wirkt ((Christian(1975))), entweder diffusionslimitiertes Wachstum ( $r^{\beta} \sim t^{1/2}$ ) oder interface-limitiertes Wachstum ( $r^{\beta} \sim t^1$ ). Beide Fälle lassen sich im Rahmen der irreversiblen Thermodynamik in Form der Ratengleichung

$\begin{displaymath} {dr^\beta \over dt} = {D \over kT} {c^\infty \over c^\beta} ... ...beta \over l_0} \Bigl(1- {r_{crit}^\beta \over r^\beta} \Bigr)\end{displaymath}$ (47)

für den zeitabhängigen Radius eines wachsenden $\beta$ -Keims zusammenfassen ((Ebeling und Ulbricht(1986)); Erklärung der Variablen und Details in (Riedel und Daßler(1990b))). Im Ergebnis zeigte sich, daß das interface-limitiertes Wachstum in der Anfangsphase dominiert, während diffusionslimitiertes Wachstum vorwiegend bei fortgeschrittener Umwandlung ( $x_{3D} \gt 35\%$ ) auftritt, vgl. Abb. 2. Eine Erklärungsmöglichkeit dafür bietet die Ausprägung von Verarmungszonen innerhalb der Lösungs-Matrix mit zunehmendem Umsatz, da die atomaren Bausteine dann über vergleichsweise längere Distanzen hin zur wachsenden Interface der neuen Phase transportiert werden müssen.

Darüberhinaus wurde mit den Experimenten generell bestätigt, daß der mit dem Phasenübergang verbundene Volumensprung zu einem deutlichen Druckabfall in der Probenkammer führt. Diese Druckveränderung ist auch kaum durch Nachführen der Stempel in Abhängigkeit vom Volumenumsatz kompensierbar, wie von (Hamaya und Akimoto(1981)) vorgeschlagen, da dies sehr wahrscheinlich zu völlig unkontrollierten Druckverhältnissen führen würde. Die günstigste Möglichkeit zum Erreichen nahezu konstanter Druckverhältnisse besteht bei einer Präparation mit Druckübertragungsmedium darin, das Verhältnis von Probenvolumen zu Kammervolumen möglichst gering zu halten (C^V_KJ in Gl. (46)), da dann der Druck im Probenraum nur geringfügig von der Probe beeinflußt wird.

Unter den (nahezu) isochoren Randbedingungen einer geschlossenen Hochdruckapparatur ist es daher nur bei Anwendung spezieller präparativer Techniken möglich, strukturelle Phasenumwandlungen bei konstanten p,T-Bedingungen ablaufen zu lassen. Sowohl die Rheologie des Stützmaterials (z.B. des Gaskets) als auch die Wärmeleitfähigkeit der Druckstempel haben einen signifikanten Einfluß auf den Prozeßverlauf und damit auf die abgeleiteten kinetischen Meßgrößen.

Next: Deformationsexperimente in der Garnet Up: Hochdruckexperimente in der Diamantstempelzelle Previous: Hochdruckmeßplatz für kinetische Experimente

Michael Riedel
10/6/1997