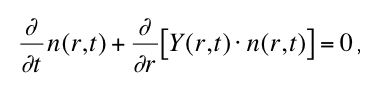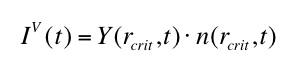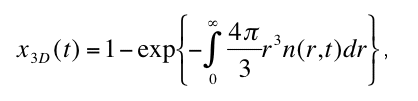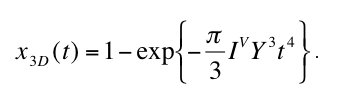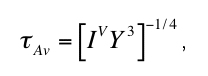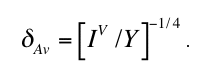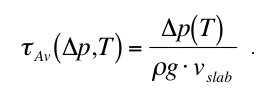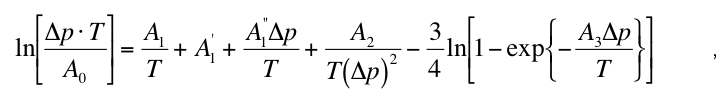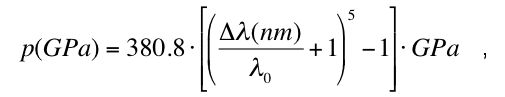DFG-Research Unit Proposal "Nanoscale Processes and Geomaterials Properties" - Project No. 3
1.0 Application for a Research Grant
DFG-Research Unit FOR741 "Nanoscale Processes and Geomaterials Properties"
1.1 Applicants
PD Dr. Michael R. Riedel (Univ. Potsdam, Geowissenschaften)
Prof. Dr. Rolf Oberhänsli (Univ. Potsdam, Geowissenschaften)
1.2 Title
Role of grain-boundary energy for the kinetics of polymorphic phase transformations
1.3 Short Title
Kinetics of polymorphic phase transformations
1.4 Research Fields
- Mineral physics
- Phase petrology
- Microstructure analysis
- Geodynamics
1.5 Expected total duration
- Research begin: 1. January 2007
- Expected duration until: 31. December 2009
1.6 Duration
1.7 Requested starting date
1.8 Summary
The kinetics of polymorphic phase transformations of selected mineral systems (calcite ->
aragonite, quartz -> coesite) is investigated with combined experimental and theoretical
methods. On the basis of the determined relevant solid-state nucleation mechanism at the
atomic scale, we use a scaling law to derive a set of critical nano-scale control parameter
such as the grain-boundary energy for solid-state nucleation from experimental observation.
For this purpose, we conduct kinetic high-pressure experiments in the diamond anvil cell.
These experiments are done under visual control and allow a precise determination of the
respective kinetic phase boundaries in dependence of temperature.
The obtained kinetic phase boundaries at the laboratory time scale are then extrapolated to
the natural time scale under subduction zone conditions. They may then be used to derive,
e.g., critical isotherms for thermo-mechanical modelling of coupled metamorphic and
deformation processes during lithosphere subduction.
2. State of research and previous work
2.1 Current state of research
Kinetics of polymorphic phase transformations - general statements
As a consequence of geodynamic or tectonic processes, minerals and mineral assemblies
may become energetically unfavourable due to changes in external physical and/or chemical
conditions. Such perturbation driven phase transformations and mineral reactions proceed to
establish a new equilibrium state that tends to minimize the system free energy. The path
along which the system develops towards equilibrium is controlled by reaction kinetics, i.e.,
by several relaxation processes driving the system back to (local) equilibrium. If one aims at
unravelling the reaction kinetics, information engraved in rock microstructures and textures is
the key. A rock sample, however, shows only the time-integrated result of the various kinetic
processes, acting sequentially or in parallel at different time scales. Only if the mechanisms
of the underlying phase transformation and mineral reactions are completely understood, it is
possible to infer the reaction kinetics from "post-mortem" rock microstructures.
The experimental and theoretical basis for the thermodynamic treatment of phase equilibria
has been well established for more than a decade now (Holland and Powell 1985, 1989,
1998, Berman 1988, Spear 1993, Connolly & Petrini 2002) and research activities on macroscopic
equilibrium thermodynamic properties of systems of geological interest have somewhat saturated.
In contrast, after the pioneering work of Lasaga and Kirkpatrick (1981) and
Rubie and Thompson (1985), the kinetic treatment of mineral reactions and phase
transformations became increasingly an active and rapidly developing field. The monograph
on "Kinetic Theory in the Earth Sciences" (Lasaga 1998) gives an account of the advances
made till 1998.
Since then, great progress in high-pressure experimentation and analytical methods made it
possible to determine kinetic properties in more detail; a number of studies, e.g., have been
performed to establish rate laws for individual polymorphic mineral reactions (Mosenfelder &
Bohlen 1997; Rubie 1998; Mosenfelder et al. 2001; Hacker et al. 2005).
Nucleation and growth processes
Polymorphic mineral reactions and phase transformations start with a nucleation stage,
followed by the growth stage after a stable nucleus has been formed. A nucleus forms by
local fluctuations of the chemical composition and/or the atomic structure. The positive free
energy associated with the formation of new interfaces and the strain energy associated with
deformation due to finite reaction volume act against the formation of a stable nucleus. The
contribution of interphase boundary energy to the specific free energy of a nucleus or grain
decreases with increasing size, and a nucleus becomes stable after it has reached a critical
size (Christian 1975). In the case of isochemical transformations, the interphase grainboundary
energy and the mechanical coupling between the newly growing and the parent
phase control reaction kinetics and microstructure evolution (Riedel and Karato 1996). In
contrast, phase transformations and mineral reactions with changes in chemical composition
require long-range mass transfer across the phase boundary ("reaction-diffusion" systems). If
the mass transfer is the rate limiting process, microstructures with a high degree of spatial
organization such as reaction bands or corona structures may develop (Joesten 1977,
Ortoleva 1994). The various ways in which mass transfer, the formation of new interfaces
and reaction induced strain may be coupled give rise to a rich inventory of microstructures
observed in natural rocks.
Sluggish kinetics and metastability
One particular problem regards the influence of a possible metastable hindrance / delay
during mineral phase transformations. Metastability is likely to cause complex behaviour
because of possibly existing strong non-linearities in the transition mechanism far from
equilibrium, beyond the validity of linear Onsager relations. A commonly held view amongst
petrologists - neglecting metastability - is, that metamorphic reactions occur close to
equilibrium, an assumption which enables P-T paths to be constructed on the basis of
observed mineral assemblages together with phase equilibria data (Spear 1989, Peacock
2000).
Due to sluggish kinetics, however, reactions may occur progressively and continuously along
a P-T-t path under disequilibrium conditions, at a rate which is mainly dependent on
temperature. For this type of process, textures of partial reaction can, in principle, be
combined with experimental kinetic data to derive quantitative information about the P-T-t
path and in particular about rates of heating or cooling. An alternative disequilibrium model
was suggested on both observations of partial reaction in metamorphic rocks and the results
of experimental studies. According to this model, mineral assemblages persist metastably
outside of their stability fields on long time scales in the absence of deformation, primarily
because of large nucleation barriers. Reaction to a lower-energy mineral assemblage
(possibly also metastable), if it occurs, takes place rapidly under pronounced disequilibrium
conditions. This type of behaviour can be documented for solid-solid and hydration reactions,
during high-pressure metamorphism for example, but may also apply in the case of
dehydration reactions and melting reactions which involve several reactant and/or product
phases (Rubie 1998). Since both responsible relaxation mechanisms, nucleation and growth,
show a largely different dependence on pressure and temperature at metamorphic
overstepping, rock microstructures are not only dependent on the P-T-path itself, but are, in
addition, dependent on the time scale of the system change, i.e., the rate of the process:
Slow metamorphic overstepping yields largely different microstructures than those
microstructures resulting from processes with fast overstepping (typically for laboratory
experiments).
Key role of nucleation processes
In a solid polycrystal, there exist in general - in addition to homogeneous nucleation - three
different types of (heterogeneous) grain-boundary nucleated reactions: new phase nucleation
either on grain boundary surface, grain edges, or grain corners. The relative importance of
each of these processes to the total nucleation rate is hereby controlled by their respective
interface energies (Cahn 1956, Christian 1975).
Nucleation rates in the solid state are particularly difficult to determine. One way to estimate
a grain-boundary nucleation rate is to count the number of product phase grains under the
electron microscope, see Figure 1 (Hacker et al. 2005). The counted number must be divided
by the sample volume to yield the nucleation rate per unit volume. The result is usually a very
large number, in the case of calcite to aragonite transition, the so calculated number is of the
order of > 10^7 nuclei m-2 s-1.
This formalism invokes a great uncertainty, since the selected measurements at the submicron TEM scale are extrapolated to mesoscopic resp. macroscopic nucleation rates over
more than 6 orders in magnitude, without suitable statistical averaging.
The obtained results are therefore likely prone to large errors.
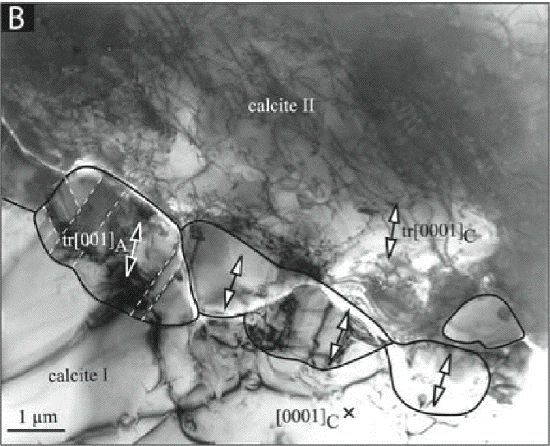
Figure 1:
Early stages of the calcite -> aragonite transformation seen with transmission electron microscopy
(Hacker et al. 2005): 5 small (1-2 mm) grain-boundary nucleated aragonite grains that have slight
misorientations with respect to each other and are topotactic with adjacent calcite crystal II
2.2 Previous work of the proponents
Michael Riedel
The research of MR has been focused on the kinetics of mineral phase transformations and
its feedback into the rheology of subducting slabs. After the study of the kinetics of the
pressure-induced B1-B2 phase transformation in the diamond-anvil cell, he investigated
within a general theoretical framework the microstructural development during nucleation and
growth (Riedel and Karato 1996, 1997). The found scaling properties were then used to
model the creep properties of subducting slabs with respect to their geodynamic behaviour in
the transition zone and the possible mechanisms of deep-focus earthquakes (Karato et al.
2001, Riedel 2006). In the context of the suggested research, MR will provide expertise in the
kinetics of high-pressure phase transformations and its coupling to continuum mechanics.
Roland Oberhänsli
The research of RO concerns the metamorphic evolution, especially of mafic and acidic highpressure rocks (Oberhänsli et al., 1985, Franz et al., 2001) Recently the focus of this
research changed towards low-grade high-pressure metamorphism of peltic metasediments
(Oberhänsli et al., 1995). In these lithologies combined studies of crystallisation and
deformation coupled with thermodynamic analyses led to the devellopement of a method
using local equilibria (Oberhänsli et al., 2002; Romer et al., 2003; Rimmelé et al., 2005). Our
studies showed that K-bearing phases that formed in equilibrium with the HP index mineral in
metapelites are well suited for age determination of the metamorphic peak conditions
(Oberhänsli et al., 1998). Now we try to date petrologically well constrained local equilibria by
39 Ar/40 Ar lased ablation methods in Potsdam.
3. Goals and working programme
3.1 Scientific objectives
Instead of attempting to estimate nucleation rates directly at the TEM level (Mosenfelder et
al. 2001, Hacker et al. 2005), one can use the information stored in the microstructure that
develops with kinetic overstepping p to derive the nucleation controlling parameter. In a
sense, this is a way to avoid the difficult problem of statistical averaging of counted
nucleation events at the TEM sub-micron scale to the mesoscopic scale - instead, the
experiment does the needed thermodynamic average.
This proposed research project aims at this approach: Knowing the relevant mechanism of
nucleation at the atomic scale, we use additional macroscopic measurements / investigations
of the phase transformation kinetics (kinetic phase boundary resp. metastable pressure
overshoot p vs. temperature T) in combination with a scaling law for the kinetic phase
boundary of isochemical uni-variant phase transitions under natural conditions (Riedel and
Karato 1997) to infer inversely the respective nucleation rate.
For this purpose, we study the transition kinetics of selected mineral systems (e.g.
calcite -> aragonite, quartz -> coesite) under in-situ conditions in a diamond-anvil cell. The amount of
metastable overshoot p(T), measured as a function of temperature T, contains nonlinearly
enciphered both nucleation rate and growth rate of the transformation process. Because
growth rates are comparatively easy to determine by various methods (e.g. digital image
processing) with sufficient accuracy, we may utilise the information stored in p(T) for the
inverse determination of the unknown nucleation rate as a function of temperature T.
This experimental strategy relies on TEM (or double-beam SEM) observations only for
identifying the correct type of solid-solid nucleation. This is, however, a crucial step of the
method, since the detailed form of the scaling relationship to be used is dependent on the
special geometry of nucleation sites (Riedel 2006). Knowing the type, we will mainly use
"macroscopic" experiments to infer the nucleation rate at the atomic scale (in a statistical
averaged sense).
Once both nucleation and growth rates are known, the overall transformation kinetics at
arbitrary time scales (i.e., as well at the laboratory time scale as at the geological time scale)
follows from an appropriate statistical combination of nucleation and growth, in dependence
of the dominating solid-solid nucleation mechanism (Cahn 1956, Christian 1975).
Specific questions to be addressed within the project
- Which solid-solid nucleation mechanisms are dominant during the selected phase
transformations (boundary/edge/corner) ? Does this dominance change with p or T ?
- How does the kinetic phase boundary p change in dependence of temperature T when
determined at the laboratory time scale?
How does the same kinetic phase boundary look like under subduction zone conditions ?
- What is the resulting microscopic nucleation rate when determined from the appropriately
chosen scaling relationship ? Together with the nucleation rate, what is the grain-boundary
interface energy (as the nano-scale controlling parameter) of the phase transformation ?
- What are the geodynamic implications of the results ? What are the "critical isotherms" for
the investigated phase transformations in a subduction zone environment, to be studied on
the basis of a thermo-mechanical model for subduction with varying thermal parameter
(implications for "fast" slabs are compared with those for "slow" slabs) ?
- What is the influence of traces of water on the reaction rates ?
Relevance of the intended research
In order to be included in quantitative thermo-mechanical modelling of geodynamic
processes, reliable kinetic data of high-pressure mineral phase transformations is needed.
This regards the whole set of activation energies and statistical pre-factors in the Arrhenius
laws for nucleation and growth and, particularly, as a critical controlling parameter, the
interface energy created by newly formed grains of the product phase ("grain-boundary
energy").
The latter parameter is, under natural conditions, not well constrained from experimental
observation. The intended project presents a novel method to derive these kinetic rate laws
by means of combined microscopic/macroscopic measurements and an appropriate kinetic
scaling law. The outcome will increase our current understanding of the complex interactions
between metamorphic and tectonic processes at subduction zones.
3.2 Working programme
We will study the kinetics of metastable polymorphic phase transformations under high
pressure. Particular emphasis is put at identifying the relevant nucleation processes at the
atomic level (grain-boundary/edge/corner nucleated reaction) by means of transmission
electron microscopy, cf. Figure 2.

Figure 2: Regions of dominant solid-solid nucleation mechanism, in dependence of metastable overstepping
(y axis) and reciprocal interphase grain-boundary energy (x axis), according to Cahn (1956).
We measure the kinetic phase boundary p (T), i.e. the metastable overstepping p of the
transformation pressure over the equilibrium value peq(T), as a function of temperature T.
This data is then used to derive, e.g., the value of the interface energy for grain-boundary
nucleated reactions and the corresponding microscopic rate laws.
Theoretical foundation
When a mineral becomes metastable due to changes in pressure or temperature, nuclei of
the new (stable) phase arise randomly both in time and space. According to the classical
nucleation theory (see, e.g., Christian 1975), the continuity equation for the number of
spherical nuclei n(r,t) with radius r at time t is then given by
where Y(r,t) is the (in general size- and time-dependent) macroscopic growth rate of the new
phase. The volume nucleation rate IV (t) defines the boundary condition
for the radius distribution function n(r,t) at the the critical nucleus size rcrit . Solving equation
(1) for n(r,t), the degree of transformation x3D in dependence of time is given by
that yields for constant Y and IV the well known Avrami equation (Christian 1975)
Equation (4) may be generalized to hold for non-homogeneous nucleation in the solid state
(Cahn 1956) and for time-varying supersaturation (Riedel and Karato 1996), where, instead
of a closed expression for x3D(t), one arrives at a set of ordinary differential equations that
has to be solved numerically for the calculation of x3D(t).
It is well established that this classical nucleation model obeys an exact dimensional scaling
which follows from the observation that IV
and Y permit the definition of a natural time and
length scale, respectively (Axe and Yamada 1986, Brandeis and Jaupart 1987)
It follows that any function specifying the spatial-temporal evolution (i.e. the microstructural
development in general) of the transforming metastable system is universal (i.e. independent
of IV and Y except a possible dimensional scale factor) when expressed in these natural units.
Riedel and Karato (1997) used this scaling property to estimate the amount of metastable
overshoot for polymorphic uni-variant phase transformations during subduction. According to
their approach, the transformation time scale AV must be of the order of the time required to
pass the metastable overshoot by subduction, z/vslab , i.e.
Equation (7) defines together with the nucleation and growth rate laws an implicit relationship
for the kinetic phase boundary pkin(t) (p(T) = metastable overshoot pkin(T) - peq(T) at a fixed
temperature) that reads
where the constants A1, A'1, A"1, A2 and A3 are given in the appendix of Riedel and Karato
(1997). The numerical solution of equation (8) for the case of the olivine to -spinel phase
transformation is plotted in the following figure, together with experimental data of three
kinetic high-pressure experiments (1 - Rubie and Brearley 1990, 2- Fujino and Irifune 1992,
3 - Rubie and Brearley 1994).
Figure 3 illustrates the rate dependency of kinetic processes: At the laboratory time scale, the
metastable overshoot must be much larger in order to obtain measurable results within the
available time of several hours or days. In contrast, natural processes evolve much slower,
with a significantly lower metastable overshoot, and may result therefore in a completely
different microstructure when a properly kinetic scaling is not taken into account.
This non-equilibrium rate dependence of transformational microstructures is analogous to the
existence of a gap in the p-T phase diagram of many minerals found at subduction zones.
Very low temperatures at high pressures seem to constitute a "forbidden zone" never
realized on Earth (Liou et al. 2000). Mineral assemblages may therefore persist metastably
outside their stability fields on long time scales in the absence of deformation, primarily
because of large nucleation barriers. Reaction to a lower-energy mineral assemblage
(possibly also metastable), if it occurs, takes place rapidly under pronounced disequilibrium
conditions. This type of behaviour has been documented for solid-solid reactions and
hydration reactions during high-pressure metamorphism (Rubie 1998).
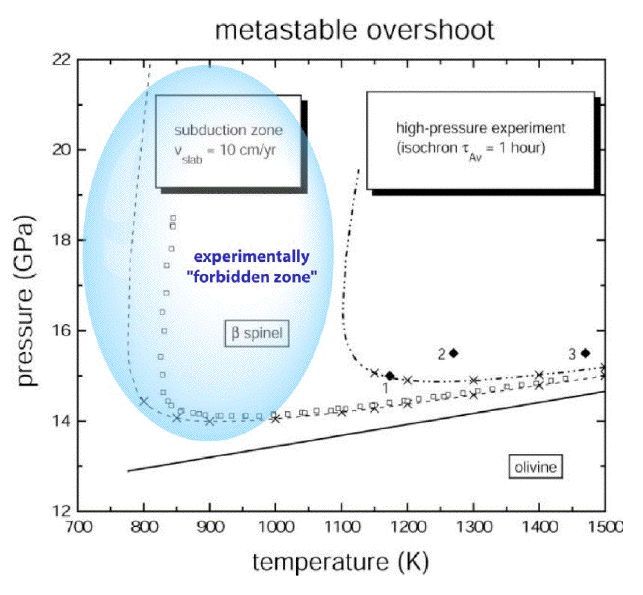
Figure 3. Calculated metastable overshoot p(T) = pkin(T) - peq(T) of forsterite over the
thermodynamic equilibrium line with -Mg2SiO4 (wadsleyite) under subduction zone conditions and
at the laboratory time
scale. The squares show the numerically calculated onset of transformation at 1% transformation
degree. The shaded area is not reachable for any high-pressure experiment because of the 7-8 orders
of magnitude difference in the kinetic time scale.
Experimental
We plan to investigate the kinetics of uni-variant phase transformations (e.g. aragonite -> calcite,
quartz -> coesite) under in-situ conditions and visual control. The experiments will be
done using a hydrothermal diamond-anvil cell of the Bassett type (Bassett et al. 1993), where
pressures up to 6 GPa can be generated at temperatures of up to 850 °C. Experiments will
be done under nearly hydrostatic load using a metal gasket and nearly isothermal conditions
throughout the sample volume of the cell.
To calibrate and monitor the pressure during the experiment, a pressure marker is added,
such as a small ruby (Al2O3:Cr3+) or strontium borate (SrB4O7:Sm2+) chip. By illumination with
a suitable laser light source, the chip emits fluorescent light at characteristic frequencies.
Knowing the pressure-induced frequency shift of the ruby R1 fluorescence line peak, the
pressure within the gasket hole is given according to (Barnett et al. 1973, Mao et al. 1978)
where = (p)-0 and 0=694.25 nm. The ruby pressure scale is linear up to 30 GPa, has
been calibrated against several independent other methods, and is accurate with an error of
less than 5% for pressures below 20 GPa (Jayaraman 1983). The advantage of the strontium
borate sensor, on the other hand, is that the temperature-induced shift of its luminescence
(-0.01 Å/K) is about 70 times smaller than the shift of the ruby sensor.
As a result of the mutual proximity of the ruby and strontium borate crystals in the sample
chamber, it is possible to collect simultaneously fluorescence spectra from both sensors. The
redundant information from the two sensors and the weak temperature dependence of the
luminescence of strontium borate allow the determination of temperatures even without the
thermocouple readings, compare Figure 4 (Datchi et al. 1997), which provides an additional
independent check for the thermocouple readings of the temperature.
As the pressure transmitting medium, we will use either a 4:1 Methanol/Ethanol mixture or
water. These pressure media have proven to be well suited for the investigation of the
proposed equilibria (Jayaraman 1983, Wang et al. 1999). Comparison of the experimental
results using different pressure media provides information on the effect of these compounds
on the kinetics of the phase transformation. Particularly, the influence of ,,dry" and hydrous
,,wet" conditions on the transition kinetics is of major geodynamic interest (e.g., Lathe et al.
2005).
The ruby fluorescence method for pressure determination is getting increasingly inaccurate
at higher temperatures because of thermal broadening in the fluorescence peaks. As an
alternative, it is possible to use the density EOS of the pressure transmitting medium to
determine the pressure in the DAC sample chamber at higher temperatures (Chou et al.
1994, Sundberg et al. 2004). Since experiments in the hydrothermal DAC are done at
isochoric conditions, the reachable pressures are determined by the initial density of the fluid
pressure medium. For a given density, the pressure is controlled by temperature, and phase
boundaries will thus be crossed on isochors. The metastable overshoot in pressure at a
given temperature can then be constructed from several experiments on different isochors.
Control of isochoric conditions is performed by comparison of the fluid density before and
after the run, e.g. by measuring liquid vapour homogenisation temperatures and using the
EOS of the used medium.
The fluid density method complements the optical method, where the pressure during the run
is monitored using the ruby and strontium borate fluorescence lines. In addition, one can
check the sample volume (isochoric condition) geometrically before and after the run, using
the wavelength separation of maxima and minima of fringes and using the volume
dependence of refractive index of water determined by Dewaele et al. [2003].

Figure 4: Fluorescence lines from two optical sensors; strontium borate and ruby. Tm is the temperature
measured from thermocouples; Tc is the temperature calculated combining the fluorescence lines of
both sensors using the metrology of Datchi et al. (1997), PR is pressure measured from ruby and PB
pressure measured from strontium borate.
In a typical heating/cooling experiment, the starting pressure remains fixed at a chosen
nominal value (e.g., between 0.6 and 2.0 GPa for the calcite/aragonite transition), and
temperature will be increased/decreased in the range 300 - 400 K. The major part of the
change of pressure within the sample chamber is then due to the effect of thermal pressure,
which occurs upon a temperature change at the quasi-isochoric conditions in the gasket hole.
A schematic overview of the used experimental setup is shown in Figure 5. During the run,
the sample can be monitored visually and the reaction progress is recorded using a video
camera. After the run, the appearance of new phase grains and the kinetic growth rate of the
product phase may be extracted directly from sequences of image snapshots by means of an
image processing system.
In addition, selected experimental runs are planned where the reaction progress is monitored
using optical micro-Raman spectroscopy. The transformation of the phase is then detected
by the appearance of new peaks in the spectra that are recorded as a function of time and
pressure overshoot.
A further option will be the monitoring of the reaction progress using X-ray diffraction
procedures. X-ray diffraction experiments with high temporal resolution can be performed at
synchrotron radiation sources that provide the photon flux necessary for such an experiment.
The use of an energy-dispersive setup that uses the continuous spectrum of a synchrotron
source provides the possibility to record the diffraction patterns within seconds to minutes.
In summarizing, all the planned kinetic experiments aim at measuring the mesoscopic kinetic
phase boundary p(T), i.e. the metastable overshoot in pressure at a given temperature T,
as accurate as possible.
Figure 5: Schematic overview of the setup for the kinetic high-pressure experiments in the hydrothermal DAC
The scaling relationship (8) is then used to derive the values of the nano-scale controlling
parameter for nucleation by inversion of the constants A1, A'1, A"1, A2 and A3. This includes
particularly the value of the grain-boundary surface energy for nucleation, which is in general,
at elevated pressures and temperatures, an only poorly constrained parameter.
Run products will be analyzed by transmission electron microscopy (TEM), or, alternatively,
by means of a double beam electron microscope, in order to get an insight into structural and
geometric features of grain- and interface-boundaries during heterogeneous nucleation
(face/edge/corner nucleation sites). The analysis at the TEM scale is crucial for the success
of this project, since the detailed form of the scaling relationship to be used is dependent on
the special geometry of nucleation sites.
Dual beam technique
A Dual beam instrument combines the options of scanning electron microscopy (SEM) with
the possibilities of precision machining by focussed ion beam technique (FIB). Modern dual
beam instruments may be equipped with a scanning transmission electron microscopy
(STEM) detector, which allows for high resolution bright- and dark field imaging using
transmitted electrons. Analytical facilities such as energy- and wave length dispersive x-ray
spectroscopy systems may be installed for elemental analysis. In addition, a system for the
detection of electron back scatter diffraction patterns may be installed.
In this project, an available dual-beam technique will largely improve the conditions for the
microstructural characterization of solid-solid nucleation processes as well as for TEM foil
preparation. As compared to conventional 2-D sectioning the option of serial sectioning at
intervals as low as 20 nanometres substantially increases the chances to find microstructures
that are diagnostic for a specific nucleation mechanisms and which may be sparsely and
irregularly distributed in 3-D.
3.4 References
- Axe J.D., Yamada Y. (1986): Scaling relations for grain autocorrelation functions during nucleation and
growth. Phys Rev B 34, 1599-1606.
- Barnett J.D., Block S., Piermarini G.J. (1973): An optical fluorescence system for quantitative pressure
measurement in the diamond-anvil cell. Rev Sci Instruments 44, 1-9.
- Bassett W.A., Shen A.H., Bucknum M., Chou I.-M. (1993): A new diamond-anvil cell for hydrothermal
studies to 2.5 GPa and from -190 to 1200 °C. Rev Sci Instruments 64, 2340-2345.
- Berman R.G. (1988): Internally consistent thermodynamic data for minerals in the system Na2O-K2OMgO-FeO-Fe2O3-Al2-O3-SiO2-TiO2-H2O-CO2. J Petrol 29, 445-522.
- Brandeis G., Jaupart C. (1987): The kinetics of nucleation and crystal growth and scaling laws for
magmatic crystallization. Contrib Mineral Petrol 96, 24-34.
- Cahn J.W. (1956): The kinetics of grain boundary nucleated reactions, Acta Metall 4, 449-459.
- Chou I.-M., Shen A.H., Bassett W.A. (1994): Applications of the diamond-anvil cell in fluid inclusion
research. In: B. De Vivo, M. L. Frezotti (eds.) Fluid Inclusions in Minerals, Methods, and
Applications, Virginia Tech, Blacksburg, VA, pp. 215-230.
- Christian J.W. (1975): The theory of transformations in metals and alloys. I. Equilibrium and general
kinetic theory. Pergamon Press, Oxford.
- Connolly J.A.D., Petrini K. (2002): An automated strategy for calculation of phase diagram sections
and retrieval of rock properties as a function of physical conditions. J Met Geol 20, 697-708.
- Datchi F., LeToullec R., Loubeyre P. (1997): Improved calibration of the SrB4O7:Sm 2+ optical pressure
gauge: Advantages at very high pressures and high temperatures. J Appl Phys 81, 3333-3339.
- Dewaele A., Eggert J.H., Loubeyre P., LeToullec R. (2003): Measurement of refractive index and
equation of state in dense He, H2, H2O, and Ne under high pressure in a diamond anvil cell. Phys
Rev B 67, 094112.
- Franz L., Romer R., Klemd R., Schmid R., Oberhänsli R., Wagner T., Dong S. (2001): Eclogite-facies
quartz veins within metabasites of the Dabie Shan (eastern China): pressure-temperature-time
deformation path, composition of the fluid phase and fluid flow during exhumation of high-pressure
rocks. Contrib Mineral Petrol 141, 332-346.
- Fujino K., Irifune T. (1992): TEM studies on the olivine to modified spinel transformation in Mg2SiO4.
In: High Pressure Research: Application to Earth and Planetary Sciences. Y. Syono and M.H.
Manghnani (eds.), Terra Publ., 237-243.
- Hacker B.R., Rubie D.C., Kirby S.H., Bohlen S.R. (2005): The calcite -> aragonite transformation in
low-Mg marble: Equilibrium relations, transformation mechanisms, and rates, J Geophys Res 110,
B03205, doi: 10.1029/2004JB003302.
- Holland T.J.B., Powell R. (1985): An internally consistent thermodynamic dataset with uncertainties
and correlations: 1: Data and results. J Met Geol 3, 343-370.
- Holland T.J.B., Powell R. (1989): An enlarged and updated internally consistent thermodynamic
dataset with uncertainties and correlations - The system K2O-Na2O-CaO-MgO-MnO-FeO-Fe2O3-
Al2O3-TiO2-SiO2-C-H2-O2. J Met Geol 8, 89-124.
- Holland T.J.B., Powell R. (1998): An internally consistent thermodynamic dataset for phases of
petrologic interest. J Met Geol 16, 309-343.
- Jayaraman A. (1983): Diamond anvil cell and high-pressure physical investigations. Rev Mod Phys 55,
65-108.
- Joesten R. (1977): Evolution of mineral assemblage zoning in diffusion metamorphism. Geochim
Cosmochim Acta 41:649-670
- Karato S., Riedel M.R., Yuen D.A. (2001): Rheological Structure and Deformation of Subducted Slabs
in the Mantle Transition Zone: Implications for Mantle Circulation and Deep Earthquakes, Phys
Earth Planet Inter 127, 83-108.
- Lasaga A.C. (1998): Kinetic Theory in the Earth Sciences. Princeton University Press, 811 pp.
- Lasaga A.C., Kirkpatrick R.J., eds. (1981) Kinetics of Geochemical Processes, Rev. Mineralogy, vol. 8,
Mineral. Society of America, Chelsea, Michigan, 398 pp.
- Lathe C., Koch-Müller M., Wirth R., van Westrenen W., Mueller H.-J., Schilling F., Lauterjung J.
(2005): The influence of OH in coesite on the kinetics of the coesite-quartz phase transition. Am
Mineral 90, 36-43.
- Liou J.G., Hacker B.R., Zhang R.Y. (2000): Into the forbidden zone. Science 287, 1215-1216.
- Mao H.K., Bell P.M., Shaner J.W., Steinberg D.J. (1978) Specific volume measurements of Cu, Mo,
Pd, and Ag and calibration of the ruby R1 fluorescence gauge from 0.06 to 1 Mbar. J Appl Phys 49,
3276.
- Mosenfelder J.L., Bohlen S.R. (1997): Kinetics of the coesite to quartz transformation. Earth Planet Sci
Lett 153, 133-147.
- Mosenfelder J.L., Marton F.C., Ross II C.R., Kerschhofer L., Rubie D.C. (2001): Experimental
constraints on the depth of olivine metastability in subducting lithosphere. Phys Earth Planet Int
127, 165-180.
- Oberhänsli R., Hunziker J.C., Martinotti G., Stern W. (1985): Geochemistry, geochronology and
petrology of Monte Mucrone: an example of Eo-Alpine eclogitisation of Permian granitoids in the
Sesia-Lanzo Zone, Western Alps, Italy. Chem Geol 52, 165-184.
- Oberhänsli R., Goffe B., Bousquet R. (1995): Record of a HP-LT metamorphic evolution in the Valais
zone: Geodynamic implications. Bolletino del Museo Regionale delle Scienze naturali Torino, 13,
221-240.
- Oberhänsli R., Candan M.P.O., Warkus F., Partzsch J., Dora O. (1998): The age of blueschist
metamorphism in the Mesozoic cover series of the Menderes Massif. Schweiz mineral petrogr Mitt
78, 309-316.
- Oberhänsli R., Martinotti G., Schmid R., Liu X. (2002): Preservation of primary volcanic textures in the
UHP terrain of Dabie Shan. Geol 30, 699-702.
- Ortoleva P. (1994): Geochemical Self-Organization. Oxford University Press, New York.
- Peacock S.M. (2000): Thermal Structure and Metamorphic Evolution of Subducting Slabs. In: Inside
the Subduction Factory, J. Eiler (ed.), American Geophysical Union, New York, pp. 7-22.
- Riedel M.R., Karato S. (1996): Microstructural development during nucleation and growth, Geophys J
Int 125, 397-414.
- Riedel M.R., Karato S. (1997) Grain-size evolution in subducted oceanic lithosphere associated with
the olivine-spinel transformation and its effects on rheology. Earth Planet Sci Lett 148, 27-43.
- Riedel M.R. (2006) Kinetic Scaling of Metastable Phase Transformations, contribution EGU06-A- 02801 (talk),
session TS3.4, General Assembly, European Geosciences Union, Vienna, April 3-7.
- Rimmelé G., Parra T., Goffé B., Oberhänsli R., Jolivet L., Candan O. (2005): Exhumation Paths of
High-Pressure-Low-Temperature Metamorphic Rocks from the Lycian Nappes and the Menderes
Massif (SW Turkey): a Multi-Equilibrium Approach. J Petrol 46, 641-669.
- Romer R.L., Wawrzenitz N., Oberhänsli R. (2003): Anomalous unradiogenic 87Sr/86Sr ratios in
ultrahigh-pressure crustal carbonates - evidence for fluid infiltration during deep subduction?
Terra Nova 15, 330-336.
- Rubie D.C. (1998): Disequilibrium during metamorphism: the role of nucleation kinetics. In: What
Drives Metamorphism and Metamorphic Reactions ?, eds. P.J. Treloar, P.J. O'Brien, The
Geological Society, Special Publication No. 138, 194-214.
- Rubie D.C., Brearley A.J. (1990): Mechanisms of the - phase transformation of Mg2SiO4 at high
temperature and pressure, Nature 348, 628-631.
- Rubie D.C., Brearley A.J. (1994): Phase transitions between - and -(Mg,Fe)2SiO4 in the Earth's
mantle: mechanisms and rheological implications, Science 264, 1445-1448.
- Rubie D.C., Thompson A.B. (1985): Kinetics of metamorphic reactions and at elevated temperatures
und pressures: An appraisal of available experimental data. In: Advances in Physical
Geochemistry, edited by A.B. Thompson and D.C. Rubie, pp. 27-79, Springer, New York.
- Spear F. (1993): Metamorphic Phase Equilibria and Pressure-Temperature-Time Paths. Monograph.
Min. Soc. Am., Washington DC, 799 pp.
- Sundberg S., Lazor P. (2004): Study of thermal pressure and phase transitions in H2O using optical
pressure sensors in the diamond anvil cell. J Phys: Condens Matter 16, 1223-1233.
- Wang X.B., Shen Z.X., Tang S.H., Kuok M.H. (1999): Near infrared excited micro-Raman spectra of
4:1 methanol-ethanol mixture and ruby fluorescence at high pressure. J Appl Phys 85, 8011-8017.
4. Funds requested
4.1 Staff
We will employ a PhD student and a student assistant at Potsdam University.
The work in this project will mainly be supervised by PD Dr. M. Riedel.
The salary of the PhD student will be according to BAT-O IIa (50%), or equivalent to TVöD.
He will have to accomplish the following tasks:
- set up and running the kinetic experiments using the diamond-anvil cell under visual control (image processing system), with a careful control of temperature conditions in the cell
- optical analysis of the run microstructures, based on digital snapshot pictures
- in-situ analysis of the kinetics of selected samples by optical spectroscopy (Raman), in
cooperation with Dr. M. Ziemann (UP)
- optional: in-situ analysis of the kinetics of selected samples by x-ray diffraction using
synchrotron radiation, in cooperation with Dr. M. Wilke (UP)
- high resolution TEM analysis on selected samples at GFZ Potsdam, in cooperation with Dr. R. Wirth (GFZ)
The successful PhD candidate will present his/her dissertation at the UP Potsdam.
Funds are also requested for student assistant (non-degree holding, without diploma). Funds
are requested on the basis of 40 hours monthly, with duration of 36 months.
The person filling this position will mainly be involved in tasks (a) and (b) and will be based at
Potsdam University.
4.2 Scientific instrumentation
The kinetic high-pressure experiments on polymorphic phase transformations will be done at
Potsdam University using an experimental setup with a hydrothermal DAC combined with a
microscope, or, alternatively, with a micro-Raman spectrometer. Some important parts of the
current equipment (image processing system, cw-DPSS-Laser system, optical analyzer for
pressure detection), however, need to be updated/replaced.
The investigation of atomic microstructures and texture development forms an essential part
of this project. This requires high resolution scanning and transmission electron microscopy
including crystal orientation imaging and element distribution mapping at highest spatial
resolution and with highest precision in sample localization. The structural characterization of
grain- and interphase boundaries requires reconstruction of the three dimensional geometrical
relationships between two adjacent grains and their common interface. This can be
done by orientation contrast imaging on serial sections taken at a spacing that is significantly
smaller then the grain size. Serial sectioning is best done by using focussed ion beam
sectioning in combination with ablation technique. The task is best accomplished by using a
DualBeam SEM/FIB machine, which allows for focussed ion beam sample preparation and
electron microscopy in a single instrument, i.e. without sample lift out between sectioning and
electron microscopy. - An application for such a DualBeam SEM/FIM machine is accompanying the
project proposals of this research unit.
4.3 Consumables
- DAC pressure cell assemblies (heating wire, cement, thermocouples, gaskets)
- replacement tungsten carbide seats and rhenium gaskets
- 2 pairs of diamond anvils (one suitable for Raman spectroscopy)
- TEM consumables (grids, film negatives, etc.)
Expenses for basic consumables (including chemicals for experiments, preparation
materials) are born by the Institute of Geosciences at Potsdam University.
4.4 Travel Expenses
Travel expenses are requested for the PhD student for participation at one international
meeting per year.
Travel expenses are also requested for the proponents M. Riedel and R. Oberhänsli for
participation in two international meetings each.
4.5 Publication costs
We envisage publication of about 3-4 papers in refereed journals. Publication costs of up to
two papers will be taken by Potsdam University. Funds are requested to cover the publication
costs for the remaining two papers.
4.6 Other costs
Not applicable.
5. Preconditions for carrying out the project
5.1 The team
Aside from the proponents, the following scientist and technicians will participate in the project:
- Dr. Lukas Keller,
Dual-Beam Scanning Electron Microscope-Lab Manager (equipment applied for), Freie Universität Berlin:
The equipment, if granted, will be operated by Dr. Lukas Keller, who is presently scholarship holder of the Swiss National Research Fonds. Dr. Keller is presently trained in Scanning Electron Microscope technique including EBSD at ETH-Zürich and University of California, Berkeley, USA.
- Dr. Richard Wirth, Senior Research Scientist, Manager of TEM Lab, GeoforschungsZentrum Potsdam
- Dr. Martin Ziemann, Senior Research Scientist, Raman spectroscopy, DAC experiments, Potsdam University
- Dr. Max Wilke, Senior Research Scientist, Synchrotron experiments with the DAC, Potsdam University
- Daniel Vollmer / Christine Fischer / Antje Musiol, Technical Engineer / Preparation Workshop / Laboratory Technician, Potsdam University
5.2 Cooperation with other scientists
- Members of the Research Unit
5.3 Foreign partners and cooperations
- Prof. Shun-ichiro Karato, phase transformation kinetics and continuum mechanics, Yale University, USA
5.4 Scientific equipment available
Experimental equipment:
- hydrothermal diamond-anvil cell (DAC of Bassett type), in combination with an optical
microscope and a temperature controller
Analytical equipment:
- Mikro-Raman spectrometer (Jobin Yvon, LabRam HR 800), Institute of Geosciences (UP)
- Powder XRD and SEM facilities, high temperature furnaces
- Preparation workshops at Institute of Geosciences (UP)
- Access to synchrotron radiation at BESSY, Hasylab beamlines
- The project plans to use GFZ's FIB and TEM facilities by about 1-2% of the available annual measurement period
5.5 Institution's general contribution
The support for consumables of Potsdam University (sample preparation, technical workshop
etc.) is given for three years.
5.6 Other requirements
None
6. Declarations
A request for funding this project has not been submitted to any other addressee. In the case
of such a request we will inform the Deutsche Forschungsgemeinschaft immediately.
The "Vertrauensdozent" of Potsdam University will be informed of this proposal.
7. Signatures
Golm, May 3, 2006
| |
(Michael Riedel) |
|
(Roland Oberhänsli) |
|