





Riedel et al. / Grain-size evolution in subducted oceanic ...
Subducted oceanic lithosphere appears to have a diversity of interaction with the mantle transition zone, which results in a complex chemical evolution and convective pattern of the Earth's mantle. An important factor that controls the fate of subducted lithosphere is its creep strength, to which grain-size reduction and latent heat release, associated with the olivine-spinel transformation might contribute important effects. The effects due to grain-size reduction can potentially be large because rheological properties of Earth materials are highly sensitive to grain size when grain size becomes sufficiently small [1][2][3].
Earlier studies suggested significant weakening of slabs due to grain-size reduction, based on laboratory observations of small grain sizes after phase transformations [1][2][4][5]. A major limitation of these previous studies, however, is the fact that grain-size reduction was observed at laboratory time scales where large driving forces for phase transformation(s) are applied to achieve a significant transformation within reasonable laboratory times (a few hours). Phase transformations in the Earth, such as in subducting slabs, occur at much longer time scales with either much smaller driving forces or at much lower temperatures. Thus, grain size after transformations in subducting slabs could be significantly different from those observed in high-pressure experiments, and the observation of small grain size in the laboratory does not necessarily imply significant grain-size reduction in the Earth's mantle. The central question then arises of how to estimate likely grain sizes for geologically relevant time scales from laboratory data.
Recently, Riedel and Karato [6] have developed a theoretical model for assessing the scaling laws of grain-size evolution during first-order phase transformations. Here, we apply this theoretical framework to estimate the grain sizes during and after the olivine-spinel transformation in subducting slabs, and, in addition, we estimate the effects of grain-size reduction on the rheological structure of slabs. For this purpose, we have also taken into account the temperature feedback from the latent heat release associated with the transformation. We assume that the rheology of peridotite is controlled either by the rheology of olivine, the weakest and most abundant mineral in the upper mantle [7][8], or by that of its high-pressure polymorphs  - or
- or  -spinel. In the two-phase region, we use a phenomenological flow law [9] to estimate the creep strength of mixed aggregates of olivine and spinel. The degree of phase transformation inside the slab is calculated on the basis of the available experimental data on the olivine-spinel transition kinetics (a compilation is given, e.g., in [10]) and the geothermal models of slabs by McKenzie [11][12], and the change in creep strength is calculated on the basis of a representative strain rate of 10-15 s-1.
-spinel. In the two-phase region, we use a phenomenological flow law [9] to estimate the creep strength of mixed aggregates of olivine and spinel. The degree of phase transformation inside the slab is calculated on the basis of the available experimental data on the olivine-spinel transition kinetics (a compilation is given, e.g., in [10]) and the geothermal models of slabs by McKenzie [11][12], and the change in creep strength is calculated on the basis of a representative strain rate of 10-15 s-1.
Our results show that spinel grain size is highly sensitive to temperature, and a large grain-size reduction and resultant significant rheological weakening is expected for cold slabs but not for warm slabs. Instead of a strong elastic "core", we find the development of a weak zone below the tip of a metastable olivine-bearing wedge in cold slabs, implying a rheological separation of the slab into two comparatively strong regions between 450 km and 600 km depth. As a result, the overall strength of a cold slab could become lower than the strength of a warm slab.
The thermal structure of subducting slabs depends primarily on the rate of subduction and on the age of the subducting oceanic lithosphere and therefore varies greatly for different subduction zones (see, e.g., [13][14]). Minimum predicted slab temperatures can be as low as 500°C at a depth where the olivine-spinel transition sets in in rapidly subducting slabs of old lithosphere. In younger slabs which subduct at relatively low velocity, the minimum temperature at this depth is likely to be much higher than 500°C. The difference between the P-T conditions inside the slab and those outside is one reason that the slab differs in mineralogy from the equilibrium mantle assemblages outside. The conventional picture of the cold slab implies, in addition, that it should also be mechanically stronger than its surrounding, and thus able to sustain and transmit higher stresses to greater depth (therefore acting as a "stress guide").
 (32681 bytes)
(32681 bytes)
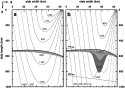
Fig. 1. Slab geometry used for the numerical model. The slab is considered as a rigid body with thickness L and a fixed length of 1000 km. The penetration angle is 45° (upper surface of the slab at the right side). Isotherms (in Kelvin) are calculated using McKenzie's model [11][12], corrected with the latent heat feedback. The bold line shows the phase equilibrium boundary of olivine and  -spinel, according to the thermodynamic data of Akaogi et al. [44] Table 1 . (a) vslab=4 cm/yr, L=85 km, Re=59.30. (b) vslab=10 cm/yr, L=85 km, Re=148.25. The metastability region of pure olivine (grey) and the region with mixed olivine-spinel aggregates (dark grey) are shown.
-spinel, according to the thermodynamic data of Akaogi et al. [44] Table 1 . (a) vslab=4 cm/yr, L=85 km, Re=59.30. (b) vslab=10 cm/yr, L=85 km, Re=148.25. The metastability region of pure olivine (grey) and the region with mixed olivine-spinel aggregates (dark grey) are shown.
A simple analytical model for the thermal profile of subduction zones is given by McKenzie's solution [11][12] for a slab of finite thickness L subducting into a hotter isothermal mantle of temperature, T0, with constant velocity vslab: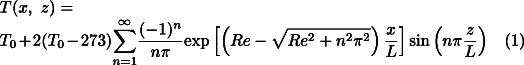
where: Re= CpvslabL/2
CpvslabL/2 is the thermal Reynolds number;
is the thermal Reynolds number;  is the density; Cp is the specific heat;
is the density; Cp is the specific heat;  is the thermal conductivity of the slab material; and the coordinates (x, z) are parallel to the slab width and length, respectively (Fig. 1 ). According to Eq. 1 , isotherms within the slab are advected downward such that the maximum depth, zmax, reached by any isotherm is proportional to the product of the vertical descent rate (trench-normal convergence rate times the sine of the dip) and the square of plate thickness, zmax~vslab.L2.
is the thermal conductivity of the slab material; and the coordinates (x, z) are parallel to the slab width and length, respectively (Fig. 1 ). According to Eq. 1 , isotherms within the slab are advected downward such that the maximum depth, zmax, reached by any isotherm is proportional to the product of the vertical descent rate (trench-normal convergence rate times the sine of the dip) and the square of plate thickness, zmax~vslab.L2.
The main portion of subducted slabs has an olivine-rich mineralogy in the upper mantle. To simplify the analysis, we assume that a subducting slab is composed of 60% olivine and that this component transforms directly into the spinel phase at a certain depth. At low temperatures, where the transformation of olivine close to the equilibrium pressure is kinetically inhibited, direct transformation to either  - or
- or  -(Mg, Fe)2SiO4 is likely to occur without any change in composition and therefore without long-range diffusion processes [10]. The growth rate of
-(Mg, Fe)2SiO4 is likely to occur without any change in composition and therefore without long-range diffusion processes [10]. The growth rate of  or
or  in this case may be described by a kinetic equation of the form:
in this case may be described by a kinetic equation of the form: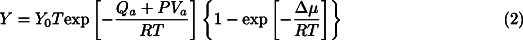
where: Qa and Va are the activation energy and activation volume for diffusion, respectively; R is the gas constant;  µ is the molar free energy difference between olivine and spinel; and Y0 is a constant.
µ is the molar free energy difference between olivine and spinel; and Y0 is a constant.
It has been shown that the  ->
-> and
and  ->
-> transition under low (mantle-like) differential stresses of less than about 1 GPa evolves predominantly as a grain-boundary nucleated process; that is, spinel grains nucleate along pre-existing olivine grain boundaries and grow afterwards at the expense of the host olivine [15][16][17]. The appropriate kinetic rate equation for this type of nucleation (compare, e.g., [18]) is:
transition under low (mantle-like) differential stresses of less than about 1 GPa evolves predominantly as a grain-boundary nucleated process; that is, spinel grains nucleate along pre-existing olivine grain boundaries and grow afterwards at the expense of the host olivine [15][16][17]. The appropriate kinetic rate equation for this type of nucleation (compare, e.g., [18]) is: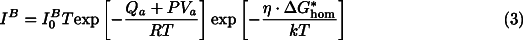
where: 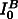 is a pre-exponential constant; k is the Boltzmann constant;
is a pre-exponential constant; k is the Boltzmann constant; 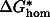 is the activation energy for the formation of a critical nucleus that depends on the thermodynamic driving force
is the activation energy for the formation of a critical nucleus that depends on the thermodynamic driving force  µ; and
µ; and  is the shape factor accounting for the lowering of
is the shape factor accounting for the lowering of 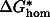 , due to the nucleation at pre-existing grain boundaries (see, e.g., [10][19]).
, due to the nucleation at pre-existing grain boundaries (see, e.g., [10][19]).
The overall transformation kinetics; that is, the volume fraction of the new phase as a function of time,  (t), depend on the rates of both nucleation and growth and are affected by the impingement of the growing grains.
(t), depend on the rates of both nucleation and growth and are affected by the impingement of the growing grains.  (t) is given by [10][18][20]:
(t) is given by [10][18][20]: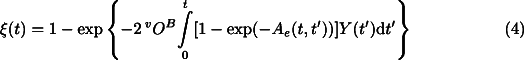
where: Ae is the increase in the extended area fraction of spinel per unit volume (see appendix for details); and vOB is the grain boundary area per unit volume of olivine. The effect of latent heat release is accounted for by including an additional term in Eq. 1 :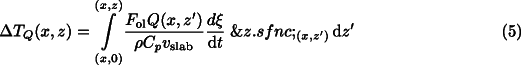
where: Fol=0.6 is the olivine content in peridotite; Q is the released heat; and d /dt is the increase in transformation degree at depth (x, z') [10][19][21].
/dt is the increase in transformation degree at depth (x, z') [10][19][21].
In order to obtain the transformed volume fraction of spinel  (t), Eq. 4 , we solve the ordinary differential equations given in Appendix A , Eq. A4 or Eq. A5 , using a 4th-order Runge-Kutta algorithm [22] along a layer of subducting lithosphere for the local P-T conditions. The effect of latent heat, Eq. 5 , is added as a correction term to T(x, z>z') at each integration step z'->z'+dz' within the slab. We neglect the thermal dissipation of the latent heat in the slab, since it is slow compared with the transformation kinetics for fast subduction [23] and would lead only to minor corrections of the McKenzie temperature profile (adiabatic heating included). Typically, the equations are integrated along the direction of subduction z within 10000 steps; that is, for a slab of 1000 km length the integration step width is 100 m.
(t), Eq. 4 , we solve the ordinary differential equations given in Appendix A , Eq. A4 or Eq. A5 , using a 4th-order Runge-Kutta algorithm [22] along a layer of subducting lithosphere for the local P-T conditions. The effect of latent heat, Eq. 5 , is added as a correction term to T(x, z>z') at each integration step z'->z'+dz' within the slab. We neglect the thermal dissipation of the latent heat in the slab, since it is slow compared with the transformation kinetics for fast subduction [23] and would lead only to minor corrections of the McKenzie temperature profile (adiabatic heating included). Typically, the equations are integrated along the direction of subduction z within 10000 steps; that is, for a slab of 1000 km length the integration step width is 100 m.

Table 1. Thermo-mechanical slab constants and kinetic parameters
Table 1 contains a compilation of the thermodynamic parameters used for the thermo-kinetic model. Note that the kinetic parameter for the non-equilibrium transition of  -Mg2SiO4 to
-Mg2SiO4 to  -phase is still subject to large uncertainties (for respective reviews, see [10][24]).
-phase is still subject to large uncertainties (for respective reviews, see [10][24]).
 (14222 bytes)
(14222 bytes)
Fig. 2. P-T phase diagram showing the kinetic phase boundaries for 1% and 99% transformation degree (dashed lines). The thick line shows the phase equilibrium of olivine and  -spinel, according to the thermodynamic data of Akaogi et al. [44]. The adiabats a-e represent the P-T paths of the coldest portion of a slab (vslab=10 cm/yr) with different thicknesses: (a) L=100 km; (b) L=90 km; (c) L=80 km; (d) L=70 km; (e) L=60 km; (f) boundary condition of the McKenzie model.
-spinel, according to the thermodynamic data of Akaogi et al. [44]. The adiabats a-e represent the P-T paths of the coldest portion of a slab (vslab=10 cm/yr) with different thicknesses: (a) L=100 km; (b) L=90 km; (c) L=80 km; (d) L=70 km; (e) L=60 km; (f) boundary condition of the McKenzie model.
The resulting kinetic phase boundaries (1% and 99% transition degree) are shown in Fig. 1 . It can be seen that the thermal structure of a slab is significantly modified by the phase transformation. The non-equilibrium phase boundary of olivine and  -spinel is advected to greater depth (boundary between the region with metastable olivine (grey) and the two-phase region (dark grey)), and the slab temperature is typically increased by 30-130°C. The P-T paths along the central (coldest) portions of slabs with increasing thicknesses are plotted in Fig. 2 . As emphasized previously [10], the latent heat production causes the transformation to occur by a runaway process, which results in steep thermal gradients around the metastable olivine wedge below 600 km depth [19].
-spinel is advected to greater depth (boundary between the region with metastable olivine (grey) and the two-phase region (dark grey)), and the slab temperature is typically increased by 30-130°C. The P-T paths along the central (coldest) portions of slabs with increasing thicknesses are plotted in Fig. 2 . As emphasized previously [10], the latent heat production causes the transformation to occur by a runaway process, which results in steep thermal gradients around the metastable olivine wedge below 600 km depth [19].
The fundamental physical processes that control grain sizes during and after a first-order phase transformation have been investigated by Riedel and Karato [6]. New grains are formed on grain boundaries in the case of heterogeneous nucleation, growing subsequently at the expense of the host phase. Upon impingement, their size is fixed, which is therefore controlled by the competition between nucleation and growth. Briefly, grain size is small when nucleation dominates over growth, and vice versa.
Theoretical considerations show that the average grain size of the product phase is given approximately by the so-called Avrami length, either in 3D ( Av, grain size after completion of the transformation), or in 2D (
Av, grain size after completion of the transformation), or in 2D (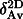 , grain diameter at the formation of continuous films), whereas the half-time of both processes is of the order of the so-called Avrami time (
, grain diameter at the formation of continuous films), whereas the half-time of both processes is of the order of the so-called Avrami time ( Av or
Av or 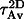 ). These scaling parameters are defined by (see [6]):
). These scaling parameters are defined by (see [6]):
and: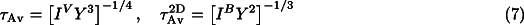
for constant nucleation and growth rates. Here, IV is the nucleation rate per unit volume; that is, the product of the grain-boundary nucleation rate, IB, and the grain-boundary area per unit volume of the reactant phase vOB:
More generally, for time-dependent P-T conditions, Eq. 6 Eq. 7 , calculated at 1% and 99% transition degree, define the range of change of average grain size and transition half-time during the transformation [6]. We shall utilize both scaling laws here: (1) to infer the spinel grain size at or near the formation of continuous films of spinel phase along the olivine grain boundaries ("spinel percolation") on the basis of Eq. 6 , and (2) to estimate the amount of metastable overshoot on the basis of Eq. 7 .
In order to estimate the creep strength of a slab during its subduction, we need to know the spinel grain size at a given point in space,  sp(x, z). For this purpose, we calculate the expected spinel grain size at the beginning of the phase transformation (1st kinetic phase boundary at
sp(x, z). For this purpose, we calculate the expected spinel grain size at the beginning of the phase transformation (1st kinetic phase boundary at  =1%) assuming that it is given by the local value of the Avrami length, Eq. 6 . Afterwards, the spinel grain size changes by two main processes: (1) crystal growth of newly formed spinel grains at the expense of the olivine host phase; and (2) competitive growth of neighbouring "old" spinel grains. In the following, we will make the assumption that the spinel contribution to the composite slab strength in the two-phase region is given by those spinel grains that first formed the continuous films at the beginning of the transformation (process 1). This seems to be justified for cold slabs with a potentially large grain-size reduction, since the dramatic drop in creep strength associated with this reduction would lead to a large viscosity contrast between the stiff matrix of predominantly olivine grains and the weak continuous spinel films percolating through this matrix. The location of this percolation transition is dependent on the extent of grain-size reduction and is therefore kinetically defined. Typically, for a grain-size reduction of 10-100, the percolation transition happens at 10-1% degree of transition [6].Competitive grain growth of fine-grained spinel after site saturation and complete impingement along the olivine grain boundaries (process 2) is likely to occur according to:
=1%) assuming that it is given by the local value of the Avrami length, Eq. 6 . Afterwards, the spinel grain size changes by two main processes: (1) crystal growth of newly formed spinel grains at the expense of the olivine host phase; and (2) competitive growth of neighbouring "old" spinel grains. In the following, we will make the assumption that the spinel contribution to the composite slab strength in the two-phase region is given by those spinel grains that first formed the continuous films at the beginning of the transformation (process 1). This seems to be justified for cold slabs with a potentially large grain-size reduction, since the dramatic drop in creep strength associated with this reduction would lead to a large viscosity contrast between the stiff matrix of predominantly olivine grains and the weak continuous spinel films percolating through this matrix. The location of this percolation transition is dependent on the extent of grain-size reduction and is therefore kinetically defined. Typically, for a grain-size reduction of 10-100, the percolation transition happens at 10-1% degree of transition [6].Competitive grain growth of fine-grained spinel after site saturation and complete impingement along the olivine grain boundaries (process 2) is likely to occur according to: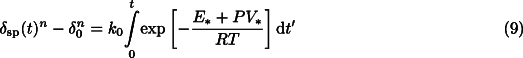
where E* and V* are activation energy and activation volume for spinel grain growth, respectively, and  0 is the grain size at
0 is the grain size at  =1% given by Eq. 6 .
=1% given by Eq. 6 .
Since there are no detailed experimental data available on the grain-growth kinetics in  - or
- or  -spinel of Mg2SiO4, we refrain here from a quantitative modelling of this process. Qualitatively, it is intuitively clear that according to Eq. 9 spinel grain growth will be very sensitive to slab temperature, and small grain size will last only to greater depth when temperatures are low; for example, in the interior of fast subducting slabs.
-spinel of Mg2SiO4, we refrain here from a quantitative modelling of this process. Qualitatively, it is intuitively clear that according to Eq. 9 spinel grain growth will be very sensitive to slab temperature, and small grain size will last only to greater depth when temperatures are low; for example, in the interior of fast subducting slabs.
Within the framework of the present model, the grain size of newly formed spinel will become very large when transformation and subsequent grain growth occur at high temperatures. These very large spinel grain sizes are not realistic, since the growing spinel grains will collide with other minerals, such as pyroxenes or garnets, when the size of newly formed grains exceeds the average size of the starting materials (~3 mm; see, e.g., [25]). At this point growth will stop and the present model will not work. Therefore, in the following we set an upper limit of 3 mm for the spinel grain size.
 (8494 bytes)
(8494 bytes)
Fig. 3. Grain-size reduction accompanying the olivine->spinel transformation and subsequent grain growth in the coldest portion of downgoing slabs. The P-T paths and the labelling as in Fig. 2 . Spinel grain growth (not included in the model) would increase again the grain size at greater depth depending on the P-T conditions.
The resulting grain-size development of spinel with depth for the different P-T paths of Fig. 2 is plotted in Fig. 3 . As it can be seen, a grain-size reduction of up to 4-5 orders of magnitude is possible for slab temperatures below 900 K. The physical reason for this dramatic drop in grain size is the large metastable overshoot,  µ, present at these low temperatures, which leads to a significant change in the balance between nucleation and growth, see discussion.
µ, present at these low temperatures, which leads to a significant change in the balance between nucleation and growth, see discussion.
The rheology of olivine is now reasonably well understood, including the effects of temperature, stress and grain size, although some critical issues, such as the effects of pressure and water, still need further investigation (for a review, see [26][27]). In contrast, the rheology of spinel or modified spinel is very poorly constrained. The only experimental data on spinel rheology is that of Vaughan and Coe [1] and Tingle et al. [28] on a germanate analogue. Some preliminary observations are also available for modified spinel [29][30] suggesting higher strength of modified spinel than olivine in the dislocation creep regime (see also [3]). In the absence of direct experimental data on the rheology of (Mg, Fe)2SiO4 spinel or modified spinel, we take the admittedly crude approximation that the rheology of spinel or modified spinel is the same as that of the spinel phase of the germanate analogue (Mg2GeO4), after the normalization of temperature by the melting temperature (T/Tm) and stress by the shear modulus ( /µ).
/µ).
Considering the strength distribution of oceanic lithosphere at upper mantle P-T conditions, slab deformation is mainly controlled by olivine creep [31][32]. For differential stresses ( ) below 200 MPa the dominant mode of deformation is power-law creep:
) below 200 MPa the dominant mode of deformation is power-law creep:
where: d /dt is the creep rate; R is the gas constant; Q1 is the creep activation energy; V1 is the creep activation volume; and C1 is a constant. For differential stresses greater than 200 MPa (low-temperature plasticity), the relevant deformation mechanism is glide-controlled creep (Peierls stress controlled dislocation glide,
/dt is the creep rate; R is the gas constant; Q1 is the creep activation energy; V1 is the creep activation volume; and C1 is a constant. For differential stresses greater than 200 MPa (low-temperature plasticity), the relevant deformation mechanism is glide-controlled creep (Peierls stress controlled dislocation glide,  p):
p):
with  p=8.5 GPa ([32]), the activation energy Q2, and a constant C2.
p=8.5 GPa ([32]), the activation energy Q2, and a constant C2.
During fast subduction, any deformation of the cold slab interior is probably described by Eq. 11 , where the values of Q2 and  p have to be modified to account for the effect of pressure. One possibility to include depth- or pressure-dependence into the creep laws is by rescaling the appropriate activation energies with the depth- or pressure-dependent melting temperature of the material (mantle solidus). We adopt here the method of Rubie [2] and rescale the corresponding parameters according to:
p have to be modified to account for the effect of pressure. One possibility to include depth- or pressure-dependence into the creep laws is by rescaling the appropriate activation energies with the depth- or pressure-dependent melting temperature of the material (mantle solidus). We adopt here the method of Rubie [2] and rescale the corresponding parameters according to:
where µ and b are the shear modulus and Burgers vector, respectively, at pressure p, and µ0 and b0 are the same parameters at 1 atm. The creep law of fine-grained spinel with grain size  sp is estimated using the experimental data on Mg2GeO4 spinel [1] according to:
sp is estimated using the experimental data on Mg2GeO4 spinel [1] according to: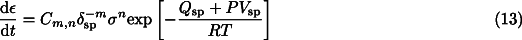
Here, Qsp and Vsp are the activation energy and activation volume for spinel creep, and Cm,n are suitable constants. We note that this rheological constitutive relation for spinel is not well constrained. For example, for oxide spinel, the dominant deformation mechanism at small grain size is linear diffusion creep rather than non-linear "superplasticity" [33]. Because of this uncertainty, we use three alternative creep laws to model the rheology of spinel: (1) Nabarro-Herring diffusion creep, assuming that diffusion occurs through the lattice (m=2, n=1); (2) Coble diffusion creep, assuming that diffusion occurs predominantly along grain boundaries (m=3, n=1); and (3) structural superplasticity, assuming that grain-boundary sliding is accommodated not by diffusion but by climb of dislocations at grain boundaries (m=2, n=2) [34]. The values of the respective constants Cm,n are chosen to fit Eq. 13 with the experimental data by Vaughan and Coe [1], a method similarly employed in [2].

Table 2. Rheological parameters for olivine and spinel
When the grain-size reduction is not large, then other deformation mechanisms such as the Peierls mechanisms or power-law creep will dominate. The creep strength in these mechanisms is not very different between olivine and spinel [3][28] and we assume that they are identical in this paper. Estimated rheological parameters for olivine and spinel are summarized in Table 2 .
In the two-phase region, we calculate the rheological properties of mixed aggregates of olivine and spinel on the basis of phenomenological flow laws for composite viscous materials. According to this approach [9], the composite creep strength is either given by:
for no grain-size reduction (when spinel forms a "load-bearing framework" within the olivine matrix), or by: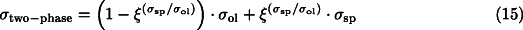
for grain-size reduction during transformation (spinel grains form a "interconnected weak layer" structure, a type of microstructure similar to the one studied theoretically in [6]). Here,  is the volume fraction of spinel, and
is the volume fraction of spinel, and  ol and
ol and  sp are the respective creep strengths of the end-member minerals. Eq. 15 has been suggested to describe the composite flow strength of quartz mylonite in quartz-feldspar granitic rock [9], where quartz forms an interconnected matrix of dynamically recrystallized grains that envelop rounded feldspar grains. The deformation stress and strain has been found to be largely partitioned into the fine-grained quartz matrix, whereas, in contrast to quartz, the feldspar grains show few traces of internal strain ([9], p. 290). Here, we argue that a similar situation could arise in the case of a large grain-size reduction resulting from the olivine-spinel phase transformation, so that most of the strain of the slab is partitioned into the relatively weak spinel phase surrounding the olivine host grains.
sp are the respective creep strengths of the end-member minerals. Eq. 15 has been suggested to describe the composite flow strength of quartz mylonite in quartz-feldspar granitic rock [9], where quartz forms an interconnected matrix of dynamically recrystallized grains that envelop rounded feldspar grains. The deformation stress and strain has been found to be largely partitioned into the fine-grained quartz matrix, whereas, in contrast to quartz, the feldspar grains show few traces of internal strain ([9], p. 290). Here, we argue that a similar situation could arise in the case of a large grain-size reduction resulting from the olivine-spinel phase transformation, so that most of the strain of the slab is partitioned into the relatively weak spinel phase surrounding the olivine host grains.
According to Eq. 15 , a significant reduction in composite flow strength is possible with only a few percent of spinel phase, provided that the contrast in creep strength between both phases is large enough ( sp<<
sp<< ol).
ol).
The most significant result of this paper is the demonstration that a large grain-size reduction can be associated with the olivine to spinel transformation when the transformation occurs at relatively low temperatures but not at high temperatures. The degree of grain-size reduction predicted by the present model for relatively cold slabs (T 900 K) is very large (down to less than 1 µm) and one expects a significant reduction in creep strength in these cases. Before we discuss potential implications, it is appropriate to interpret our results and compare them with some laboratory observations.
900 K) is very large (down to less than 1 µm) and one expects a significant reduction in creep strength in these cases. Before we discuss potential implications, it is appropriate to interpret our results and compare them with some laboratory observations.
 (19560 bytes)
(19560 bytes)
Fig. 4. Arrhenius plot of spinel grain size (logarithmic scale) vs. temperature (reciprocal scale), both numerically determined at the first kinetic phase boundary ( =1%) for different slab thicknesses. The symbols show the values obtained of spinel grain size at
=1%) for different slab thicknesses. The symbols show the values obtained of spinel grain size at  =1% for different subducting layers of lithosphere across the slab. Above 900 K, they follow an Arrhenius dependence with an apparent "activation energy" of about 412 kJ/mol (branch A). Shown as a thick solid line is the semi-analytical solution of Eq. A6 , predicting a slightly higher value of 447 kJ/mol. Note that, within the metastable wedge, the apparent "activation energy" for spinel grain size can be negative (branch B). Predicted grain sizes exceeding ~3 mm are not realistic since the presence of secondary phases such as pyroxenes and garnets prevents the formation of larger spinel grains.
=1% for different subducting layers of lithosphere across the slab. Above 900 K, they follow an Arrhenius dependence with an apparent "activation energy" of about 412 kJ/mol (branch A). Shown as a thick solid line is the semi-analytical solution of Eq. A6 , predicting a slightly higher value of 447 kJ/mol. Note that, within the metastable wedge, the apparent "activation energy" for spinel grain size can be negative (branch B). Predicted grain sizes exceeding ~3 mm are not realistic since the presence of secondary phases such as pyroxenes and garnets prevents the formation of larger spinel grains.
The numerically calculated spinel grain sizes  0 at
0 at  =1% (near the percolation threshold) are plotted as a function of temperature in Fig. 4 . The results include slabs with different initial temperature distributions (variable thicknesses) and different subduction velocities. They show that the dependence of spinel grain size on slab temperature consists of two different branches, in close relationship to the existence of two branches of the kinetic phase boundary shown in Fig. 2 . At high temperatures (branch A), spinel grain size depends on temperature as
=1% (near the percolation threshold) are plotted as a function of temperature in Fig. 4 . The results include slabs with different initial temperature distributions (variable thicknesses) and different subduction velocities. They show that the dependence of spinel grain size on slab temperature consists of two different branches, in close relationship to the existence of two branches of the kinetic phase boundary shown in Fig. 2 . At high temperatures (branch A), spinel grain size depends on temperature as  0~exp(-E*/RT), whereas in cold portions of slabs (branch B), a more complicated behaviour is found: At lower temperatures, the logarithmic plot of grain size vs. T has a negative slope; that is, grain size can decrease with temperature in a certain range.
0~exp(-E*/RT), whereas in cold portions of slabs (branch B), a more complicated behaviour is found: At lower temperatures, the logarithmic plot of grain size vs. T has a negative slope; that is, grain size can decrease with temperature in a certain range.
To interpret this observation and to compare the results with laboratory experiments, we rewrite Eq. 6 as:
Now, within the high temperature branch of the kinetic phase boundary (branch A), the transformation occurs near to equilibrium and the distance between kinetic and equilibrium phase boundary depends only weakly on temperature. The main effect of temperature on grain size comes from the growth rate term (Y) and hence:
Eq. 17 has an Arrhenius type temperature dependence with an apparent "activation energy" similar to that of growth kinetics, in accordance with the numerical results shown in Fig. 4 .
Within the low temperature branch (branch B), the transformation occurs only at a significant overstepping over equilibrium. The amount of metastable overshoot,  P, necessary to start the transformation kinetics can be estimated on the basis of a time scale argument [6][35]: The transformation time scale,
P, necessary to start the transformation kinetics can be estimated on the basis of a time scale argument [6][35]: The transformation time scale,  Av, must be of the order of the time required to pass the overshoot:
Av, must be of the order of the time required to pass the overshoot:
Together with the nucleation and growth rates according to Eq. 2 and Eq. 3 , Eq. 18 defines an implicit relationship for the kinetic phase boundary Pkin(T) ( P
P metastable overshoot, Pkin-Peq) in dependence of temperature, T, which can be solved numerically (a detailed analysis is given in Appendix A ).
metastable overshoot, Pkin-Peq) in dependence of temperature, T, which can be solved numerically (a detailed analysis is given in Appendix A ).
 (17826 bytes)
(17826 bytes)
Fig. 5. Calculated metastable overshoot  P=Pkin-Peq of olivine over the equilibrium pressure with
P=Pkin-Peq of olivine over the equilibrium pressure with  -Mg2SiO4 (Eq. A6 ) under subduction zone conditions (dashed line). The squares show the numerically calculated onset of transformation at
-Mg2SiO4 (Eq. A6 ) under subduction zone conditions (dashed line). The squares show the numerically calculated onset of transformation at  =1% for a slab with thickness L=100 km (integration of the differential Eq. A4 Eq. A5 , thick line=phase equilibrium). For comparison, the isochron
=1% for a slab with thickness L=100 km (integration of the differential Eq. A4 Eq. A5 , thick line=phase equilibrium). For comparison, the isochron  Av=1 h is included, showing the expected location of the kinetic phase boundary at the laboratory time scale (dash-dotted curve). At the geological time-scale, wedge formation sets in at temperatures below 850 K. A compilation of some spinel grain sizes at selected P-T conditions (crosses) is given in Table 3 ; solid diamonds mark the reported P-T conditions of three different high pressure experiments: (1) P=15 GPa, T=1173 K [36], spinel grain size
Av=1 h is included, showing the expected location of the kinetic phase boundary at the laboratory time scale (dash-dotted curve). At the geological time-scale, wedge formation sets in at temperatures below 850 K. A compilation of some spinel grain sizes at selected P-T conditions (crosses) is given in Table 3 ; solid diamonds mark the reported P-T conditions of three different high pressure experiments: (1) P=15 GPa, T=1173 K [36], spinel grain size 1 µm, Eq. 6 predicts 1.8 µm; (2) P=15.5 GPa, T=1273 K [16], spinel grain size
1 µm, Eq. 6 predicts 1.8 µm; (2) P=15.5 GPa, T=1273 K [16], spinel grain size 1.8 µm, Eq. 6 predicts 0.4 µm, (3) P=15.5 GPa, T=1473 K [46], spinel grain size not mentioned, Eq. 6 predicts 4.6 µm.
1.8 µm, Eq. 6 predicts 0.4 µm, (3) P=15.5 GPa, T=1473 K [46], spinel grain size not mentioned, Eq. 6 predicts 4.6 µm.
We find the solution obtained,  P(T), on the basis of Eq. 18 in good agreement with the numerical result of the Runge-Kutta integration of the kinetic differential equations, where we calculate
P(T), on the basis of Eq. 18 in good agreement with the numerical result of the Runge-Kutta integration of the kinetic differential equations, where we calculate  P(T) under the assumption that Pkin is given by the pressure value at 1% transition degree. Both calculation schemes show that metastable hindrance can cause an overshoot of up to 200 km and more at temperatures below 850 K, see Fig. 5 . Typically,
P(T) under the assumption that Pkin is given by the pressure value at 1% transition degree. Both calculation schemes show that metastable hindrance can cause an overshoot of up to 200 km and more at temperatures below 850 K, see Fig. 5 . Typically,  P ranges between 0.7 and 0.4 GPa at temperatures between 950 and 1300 K. Below 900 K, the persistence of metastable olivine to greater depth leads to a different T dependence. Analytically, it follows from Eq. 6 at
P ranges between 0.7 and 0.4 GPa at temperatures between 950 and 1300 K. Below 900 K, the persistence of metastable olivine to greater depth leads to a different T dependence. Analytically, it follows from Eq. 6 at  µ>>RT:
µ>>RT:
with c1=16

 3
3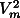 /9k, and
/9k, and  µ(T) is an almost linearly increasing function of T (see Appendix A ). Eq. 19 predicts a minimum grain size of
µ(T) is an almost linearly increasing function of T (see Appendix A ). Eq. 19 predicts a minimum grain size of  0~(I0B/Y0)-1/3 at very large overshoots, whereas at intermediate
0~(I0B/Y0)-1/3 at very large overshoots, whereas at intermediate  µ
µ RT, it predicts a grain size decrease with increasing temperature (branch B of Fig. 4 ).
RT, it predicts a grain size decrease with increasing temperature (branch B of Fig. 4 ).

Table 3. Spinel grain size: comparison with laboratory data
The present results may also be compared with some experimental observations. Rubie and Brearley [36] and Brearley et al. [37] transformed hot pressed forsterite powder to its high-pressure polymorphs by gradually increasing the pressure into the spinel stability field (P=15 GPa) at nearly constant temperatures (T=1173 K) at the laboratory time scale (duration of the experiments 1 h and 5 h, respectively). Their experimental data on grain size of modified spinel phase should therefore be comparable with the here presented grain-size estimations based on the Avrami length taken at these P-T conditions. The results are shown in Fig. 5 and Table 3 . There appears to be a reasonable agreement between the experimental observations and the theoretical estimations, both as to the reachable P-T conditions at the laboratory time-scale as well as to the reported spinel grain sizes. The large difference between laboratory and geologic time scale results hereby in large grain-size differences at the same reference temperature (according to Eq. A9 ), but these differences are, to a great extent, compensated again by the entirely different temperature conditions.
We point out here, however, that the grain-size estimations presented are largely based on the current understanding of the transformation process from olivine to spinel under subduction zone conditions (as reviewed, e.g., in [38][24]). More recent work of Kerschhofer et al. [39] shows that intracrystalline nucleation of spinel may become important at large metastable overshoots of about 18-20 GPa and relatively low temperatures of 1000-1400°C. As of now, since these newly found results are not quantified yet, we state only that an additional shear-induced coherent nucleation mechanism would, of course, affect the above grain size estimations, and that these new findings could be of particular importance for the overall transition kinetics; possible effects could be either a considerable narrowing of the depth of the region of olivine-spinel coexistence or a reduction in the metastable overshoot of olivine in cold slabs.
 (19034 bytes)
(19034 bytes)
Fig. 6. Creep strength of the slab shown in Fig. 1 along its coldest part (slab thickness 85 km) below 400 km. The grain size reduction produces a strength drop of several orders in magnitude, in dependence of the relevant spinel creep mechanism. An average strain rate of 10-15 s-1 is assumed uniformly across the slab.
 (43939 bytes)
(43939 bytes)
Fig. 7. Calculated strength profile of the slab shown in Fig. 1 on the basis of a Nabarro-Herring creep mechanism for spinel (m=2 and n=1 in Eq. 13 ). The creep strength of spinel is assumed to be bounded by the olivine creep strength within the slab. The grey area shows the slab portions with a creep strength higher than 100 MPa; the dark grey shows the slab portions with a creep strength higher than 200 MPa. Note the dramatic strength drop below the tip of the metastable wedge. Spinel grain growth (not included in the model) would cause a significant decrease in the size of the weak zone below the metastable wedge. The two arrows indicate the possible effect of a sustainable pressure drop in the cold interior of fast slabs (see discussion).
The strong dependence of spinel grain size on temperature under the P-T conditions of subducting slabs gives rise to the surprising possibility that the effective viscosity of the slab after the olivine-spinel phase transformation could be higher at higher temperatures (see also the discussion by Rubie and Ross [10], p. 238). In order to investigate this possibility more quantitatively, we plot the creep strength within the slab for a representative strain rate of 10-15 s-1 on the basis of appropriate constitutive equations for olivine and spinel creep in Fig. 6 Fig. 7 .
Fig. 6 shows the creep strength of the slab vs. depth along the coldest portion for three different spinel creep laws and two different subduction velocities. As can be seen, the creep strength in the central portions of fast slabs drops down by several orders of magnitude and assumes a minimum near to the depth where the phase transformation is almost completed (2nd kinetic phase boundary,  =99%). This behaviour appears to be typical for all three grain-size sensitive creep laws (Nabarro-Herring creep, Coble creep and superplasticity, compare Table 2 ). In contrast, the creep strength of a slow slab remains well above these values, suggesting that a warm slab could be (partially) stronger than a cold slab.
=99%). This behaviour appears to be typical for all three grain-size sensitive creep laws (Nabarro-Herring creep, Coble creep and superplasticity, compare Table 2 ). In contrast, the creep strength of a slow slab remains well above these values, suggesting that a warm slab could be (partially) stronger than a cold slab.
In Fig. 7 , we extend this figure into a two-dimensional plot in order to show the rheological structure of a whole slab (Nabarro-Herring creep only). As expected from Fig. 6 , a localized weak zone develops below the tip of the metastable olivine wedge. This weak zone can occupy up to 20% of the slab interior, thus dividing the slab into two comparatively stronger layers at the top and bottom, at depths between 450 and 600 km. In this way it is acting as a kind of low pressure inclusion within the slab body, since the stronger bottom and top layers prevent the undelayed accommodation of the associated density increase by the surrounding hotter mantle. The likely existence of complex internal states of stress produced by the effects of the volume changes accompanying the transformation of peridotite to the transition zone mineral assemblage has also been emphasized recently by Kirby and Okal [40].
Finally, we comment briefly on some geodynamic implications of the present study. It has been argued that deep earthquake activities are related to the transformation of metastable olivine to the modified or spinel phase, since seismicity is high in slabs where metastable olivine is considered to occur [5][38][24][41][42]. Deep earthquakes are hereby believed to occur as a result of the instability of deformation in the ductile regime. The present results provide some insight into the possible mechanisms of deep earthquakes. Combined with the results of thermal models of slabs [19], we propose that the nature of instabilities associated with the olivine-spinel transformation is fundamentally different between the cold and warm branches of the kinetic phase boundary and that instabilities will occur only when the transformation occurs in the cold branch. Our studies suggest two instability mechanisms. One is thermal runaway due to the latent heat release [19]. We have shown that the latent heat release causes positive feedback only when the transformation occurs in the cold branch but not in the hot branch [19], compare also Fig. 2 .
Similarly, the effects of grain-size reduction to cause softening and hence instability will be important only in the cold branch because significant grain-size reduction occurs only at relatively low temperatures. In addition, since the degree of grain-size reduction increases with temperature in this regime (see Fig. 4 and Eq. 19 ), a self-accelerating instability is prone to occur there. Thus, both the effects of latent heat and of grain-size reduction tend to lead to shear instability in the cold branch but not in the hot branch.
Our theoretical calculations have shown that the olivine-spinel transformation in subducting slabs can indeed result in a significant grain-size reduction and resultant rheological weakening. We have also shown that the effect is highly sensitive to temperature at which the phase transformation occurs. These predictions are consistent with experimental observations that the size of grains formed by nucleation and growth tends to be small when transformation occurs at relatively low temperatures.
The present results, however, have some limitations which have to be further investigated in future studies. First, some parameters in transformation kinetics are not well constrained. In particular, parameters related to nucleation processes are poorly constrained [10][39]. This leads to large uncertainties in grain size in the low temperature regime (see Eq. 19 ), although it will not affect the results in the high temperature regime (Eq. 17 ). In addition, changes in the nucleation and growth rates due to the accompanying pressure drop are neglected. Second, the flow laws for spinel in the grain-size sensitive regime are poorly constrained, which leads to large uncertainties in estimated strength from grain size and temperature (and pressure), Fig. 6 Fig. 7 . Third, the temperatures in slabs are also only poorly constrained, the main uncertainties include the effects of shear heating and of latent heat. Thus, the details of the present results must be taken with caution. However, the notion of large rheological weakening due to grain-size reduction in cold slabs seems robust and should be taken into account in any models of slab dynamics.
Copyright © 1997 Elsevier Science B.V., Amsterdam. All Rights Reserved.






 - or
- or  -spinel. In the two-phase region, we use a phenomenological flow law [9] to estimate the creep strength of mixed aggregates of olivine and spinel. The degree of phase transformation inside the slab is calculated on the basis of the available experimental data on the olivine-spinel transition kinetics (a compilation is given, e.g., in [10]) and the geothermal models of slabs by McKenzie [11][12], and the change in creep strength is calculated on the basis of a representative strain rate of 10-15 s-1.
-spinel. In the two-phase region, we use a phenomenological flow law [9] to estimate the creep strength of mixed aggregates of olivine and spinel. The degree of phase transformation inside the slab is calculated on the basis of the available experimental data on the olivine-spinel transition kinetics (a compilation is given, e.g., in [10]) and the geothermal models of slabs by McKenzie [11][12], and the change in creep strength is calculated on the basis of a representative strain rate of 10-15 s-1.






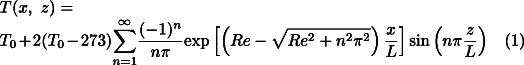
 CpvslabL/2
CpvslabL/2 is the thermal Reynolds number;
is the thermal Reynolds number; 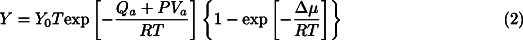
 µ is the molar free energy difference between olivine and spinel; and Y0 is a constant.
µ is the molar free energy difference between olivine and spinel; and Y0 is a constant. ->
->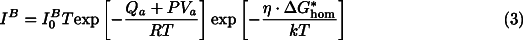
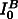 is a pre-exponential constant; k is the Boltzmann constant;
is a pre-exponential constant; k is the Boltzmann constant; 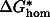 is the activation energy for the formation of a critical nucleus that depends on the thermodynamic driving force
is the activation energy for the formation of a critical nucleus that depends on the thermodynamic driving force  is the shape factor accounting for the lowering of
is the shape factor accounting for the lowering of  (t), depend on the rates of both nucleation and growth and are affected by the impingement of the growing grains.
(t), depend on the rates of both nucleation and growth and are affected by the impingement of the growing grains. 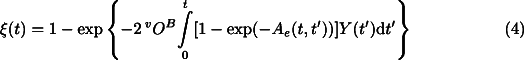
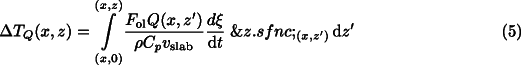


 Av, grain size after completion of the transformation), or in 2D (
Av, grain size after completion of the transformation), or in 2D (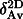 , grain diameter at the formation of continuous films), whereas the half-time of both processes is of the order of the so-called Avrami time (
, grain diameter at the formation of continuous films), whereas the half-time of both processes is of the order of the so-called Avrami time ( Av or
Av or 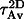 ). These scaling parameters are defined by (see
). These scaling parameters are defined by (see 
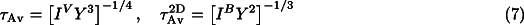

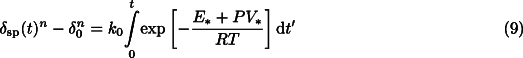

 /µ).
/µ).
 /dt is the creep rate; R is the gas constant; Q1 is the creep activation energy; V1 is the creep activation volume; and C1 is a constant. For differential stresses greater than 200 MPa (low-temperature plasticity), the relevant deformation mechanism is glide-controlled creep (Peierls stress controlled dislocation glide,
/dt is the creep rate; R is the gas constant; Q1 is the creep activation energy; V1 is the creep activation volume; and C1 is a constant. For differential stresses greater than 200 MPa (low-temperature plasticity), the relevant deformation mechanism is glide-controlled creep (Peierls stress controlled dislocation glide, 

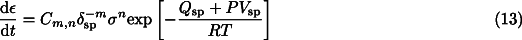

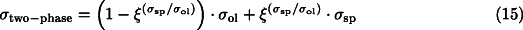
 900 K) is very large (down to less than 1 µm) and one expects a significant reduction in creep strength in these cases. Before we discuss potential implications, it is appropriate to interpret our results and compare them with some laboratory observations.
900 K) is very large (down to less than 1 µm) and one expects a significant reduction in creep strength in these cases. Before we discuss potential implications, it is appropriate to interpret our results and compare them with some laboratory observations.



 metastable overshoot, Pkin-Peq) in dependence of temperature, T, which can be solved numerically (a detailed analysis is given in
metastable overshoot, Pkin-Peq) in dependence of temperature, T, which can be solved numerically (a detailed analysis is given in 
 1 µm, Eq. 6 predicts 1.8 µm; (2) P=15.5 GPa, T=1273 K [16], spinel grain size
1 µm, Eq. 6 predicts 1.8 µm; (2) P=15.5 GPa, T=1273 K [16], spinel grain size

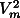 /9k, and
/9k, and  RT, it predicts a grain size decrease with increasing temperature (branch B of
RT, it predicts a grain size decrease with increasing temperature (branch B of 
