 (t), under constant P-T conditions for grain boundary nucleated reactions was derived by Cahn [20] as:
(t), under constant P-T conditions for grain boundary nucleated reactions was derived by Cahn [20] as:
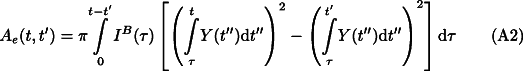
 ) as the grain boundary nucleation rate of spinel, and Eq. A1 is generalized to:
) as the grain boundary nucleation rate of spinel, and Eq. A1 is generalized to: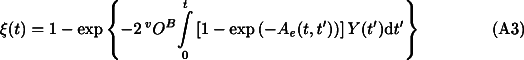






We give here a brief derivation of the kinetic equations used in the modelling section. The overall tranformation rate,  (t), under constant P-T conditions for grain boundary nucleated reactions was derived by Cahn [20] as:
(t), under constant P-T conditions for grain boundary nucleated reactions was derived by Cahn [20] as:
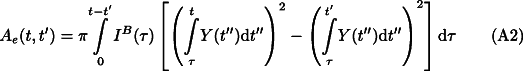
 ) as the grain boundary nucleation rate of spinel, and Eq. A1 is generalized to:
) as the grain boundary nucleation rate of spinel, and Eq. A1 is generalized to: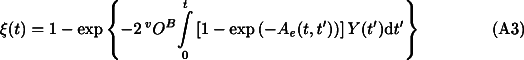
Here, we simplify the kinetic analysis on the basis of the following observation: At starting transformation (undersaturated nucleation), the overall transition kinetics are indistinguishable from a homogeneous nucleation and growth process. This can be shown to be valid as long as the kinetically determined Avrami length  Av is larger or in the same order as the initial grain size of the host phase, Lini~1/vOB [6]. At later stages, site saturation along the preferred nucleation sites at grain boundaries sets in and leads to linear growth of new phase grains at the already transformed grain boundaries. It has been shown [20], that this change (site saturation and change from 3D->1D growth) occurs in a rather narrow time interval during the transformation, in the vicinity of the percolation point
Av is larger or in the same order as the initial grain size of the host phase, Lini~1/vOB [6]. At later stages, site saturation along the preferred nucleation sites at grain boundaries sets in and leads to linear growth of new phase grains at the already transformed grain boundaries. It has been shown [20], that this change (site saturation and change from 3D->1D growth) occurs in a rather narrow time interval during the transformation, in the vicinity of the percolation point  Per of the new phase grains. As a consequence, it is possible to solve the two limiting cases separatedly instead of Eq. A2 Eq. A3 , and to switch between both cases numerically, depending on the calculated transformed volume degree
Per of the new phase grains. As a consequence, it is possible to solve the two limiting cases separatedly instead of Eq. A2 Eq. A3 , and to switch between both cases numerically, depending on the calculated transformed volume degree  (t)=1-exp(-X3D(t)); X3D, X2D, X1D, and X0D denote in the following the total grain volume, grain area, grain diameter, and grain number of the product phase (as defined in [6], p. 398).
(t)=1-exp(-X3D(t)); X3D, X2D, X1D, and X0D denote in the following the total grain volume, grain area, grain diameter, and grain number of the product phase (as defined in [6], p. 398).
Case (1): Homogeneous nucleation,  (t)
(t)
 Per(exp[-Ae]
Per(exp[-Ae] 1-Ae):
1-Ae):
Case (2): Site-saturated nucleation,  (t)
(t)
 Per (exp[-Ae]
Per (exp[-Ae] 0):
0):
The percolation threshold for grain boundary nucleated reactions,  Per, is dependent on the Lini/
Per, is dependent on the Lini/ Av ratio of the host phase and is calculated on the basis of the numerical simulation algorithm described in [6]. For a grain-size reduction of several orders in magnitude (i.e.,
Av ratio of the host phase and is calculated on the basis of the numerical simulation algorithm described in [6]. For a grain-size reduction of several orders in magnitude (i.e.,  Av<<Lini) it is well below
Av<<Lini) it is well below  ~1%, and Eq. A5 applies almost everywhere in the two-phase region of the slab.
~1%, and Eq. A5 applies almost everywhere in the two-phase region of the slab.
The metastable overshoot,  P, follows from Eq. 18 , combined with Eq. 2 Eq. 3 and Eq. 7 . After insertion, one obtains the following transcendental equation for
P, follows from Eq. 18 , combined with Eq. 2 Eq. 3 and Eq. 7 . After insertion, one obtains the following transcendental equation for  P(T):
P(T):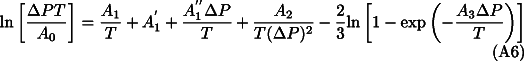
 gvslab/
gvslab/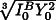 , A1=(Qa+P0Va)/R, A1'=
, A1=(Qa+P0Va)/R, A1'= SVa/
SVa/ VR, A1''=Va/R, A2=16
VR, A1''=Va/R, A2=16

 3
3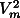 /9k(
/9k( V)2, and A3=
V)2, and A3= V/R.
V/R.
Eq. A6 is numerically solved with a Newton-Raphson iteration algorithm. It has a single solution for A1''=0; that is, for vanishing pressure effect on the activation energy. At finite A1'', a second solution appears for overcritical overpressures  P>
P> Pcrit. The critical overpressure
Pcrit. The critical overpressure  Pcrit, where the kinetic phase boundary bifurcates in two branches (d
Pcrit, where the kinetic phase boundary bifurcates in two branches (d P/dT->-
P/dT->- ), is approximately given with:
), is approximately given with: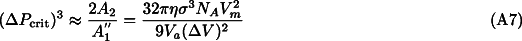
 µ<<RT, we find:
µ<<RT, we find: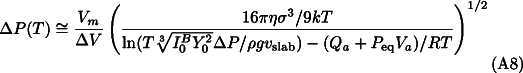
The expected spinel grain size at  µ<<RT is given with (Eq. 17 ):
µ<<RT is given with (Eq. 17 ):
Eq. A9 is an Arrhenius relationship with an apparent activation energy, Qgs, close to the activation energy for diffusion of atomic units to the growing interface, Qa. Neglecting the weak dependence of  P on T, Qgs has the order of magnitude:
P on T, Qgs has the order of magnitude:
 µ>>RT, we obtain (Eq. 19 ):
µ>>RT, we obtain (Eq. 19 ):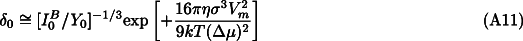
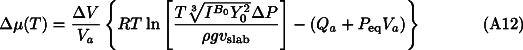
The critical depth that separates both cases Eq. A9 Eq. A11 can be found from the condition  µ~RT. This depth is for the olivine-spinel transformation at 850 K given by:
µ~RT. This depth is for the olivine-spinel transformation at 850 K given by:





