Criticality of Subducting Slabs

Next: References

Criticality of Subducting Slabs

Michael R. Riedel ¹, Shun-ichiro Karato ², and David A. Yuen $^{2, \, 3}$

¹ GeoForschungsZentrum Potsdam, Telegrafenberg, D-14473 Potsdam, FR Germany

² Department of Geology and Geophysics, University of Minnesota, Minneapolis, MN 55455, U. S.A.

³ Minnesota Supercomputer Institute, Minneapolis, MN 55415, U.S.A.

ABSTRACT We calculate the amount of viscous dissipation during subduction of a lithospheric plate as constrained by experimental rock mechanics. The maximum bending moment M_crit that can be sustained by a slab is of the order of 10¹⁹ Nm per m according to $M_{crit} \cong \sigma_p * h^2/4$ ,where $\sigma_p$ is the Peierl's stress limit of olivine and h is the slab thickness. Near M_crit, the amount of viscous dissipation grows strongly as a consequence of a lattice instability of mantle minerals (dislocation glide in olivine). The value of M_crit is about 1-2 orders of magnitude too high to be reached by a ridge push of typically 10¹² N per m at convergent plate boundaries, but unusual tectonic settings like a thick sedimentary load of the lithosphere or a shallow angle of slab penetration at the transition zone can help to overstep this bending moment threshold. The immediate consequence is a sudden drop of the effective viscosity to below 10²¹ Pas, so that the observed weakening effect serves as a self-regulating mechanism to adjust plate tectonics on Earth against strong viscous resistance forces.

1. Introduction The bending strength of subducted slabs imposes important constraints on the global style of mantle convection. In the transitional regime between an isoviscous and a ``rigid lid'' type convection that is expected to exist on Earth [1], significant resistance is offered to the viscous mantle flow by the energy dissipation occuring in the upper thermal boundary layer. The strong viscosity of the cold surface layers is therefore likely to control the rate of surface recycling and the efficiency of cooling of the planet.

Recently, Conrad & Hager [2] calculated the partitioning of viscous dissipation between a subducting slab and its environment in the steady state limit. They found that the energy dissipation within the subducting oceanic lithosphere may consume considerable amounts of energy of the coupled mantle/slab system, up to 60% of the potential energy of a descending slab for a slab thickness of 100 km. One limitation of their approach is that they restrict themselves to an effectively linear constutitive relation between stress and strainrate of the slab material. The rheology of slab material, however, is likely to change strongly across their thickness and with depth due to large variations in temperature and mineralogy. In addition, non-equilibrium effects related to mineral transformations such as latent heat release and kinetic grain-size reduction as well as the effects of persisting metastable phases may result in very complex patterns of slab rheology. It has been shown recently [3] that, in a certain range of the external acting bending moment on the slab, the creep properties of the slab material can vary quite significantly with the applied external bending moment, because of the stress dependence of nonlinear creep equations and the non-linear feedback mechanisms of the phase transition kinetics.

Here, we study this observation in more detail using the moment balance formulation suggested by Karato et al. [3] to calculate the stress - strain in a bended slab. Our aim is to show that because of the nonlinear feedback mechanisms, slab rheology acts as a kind of self-regulating mechanism, leading the coupled mantle-lithosphere during subduction into a ``self-organized'' critical state, similarly to that what is observed in the classical sandpile model [4]. We calculate the amount of dissipation within a subducting slab and find that for a threshold bending moment on the order of 10¹⁹ N, a critical dependence of viscous dissipation vs. moment appears so that the average shear-heating rate of the slab diverges with a super-power law. We find that this behaviour is largely independent of specific materials properties and that it should be present therefore at any subduction zone.

We assume a pure viscous rheology for the slab material. As pointed out by Conrad & Hager [2], the presence of permanent deformation in a subducting slab is indicative of the rheology that controls the slab's behaviour. If only elastic bending is assumed, a simple estimation shows that the maximum bending stress in the plate must be of order of several GPa for a radius of curvature of $\sim$ 200 km [5]. This is about an order of magnitude larger than the maximum strength of oceanic lithosphere so that at most only 10% of elastic bending stresses can be supported. The remaining stress must be relaxed by permanent deformation, i.e. viscous energy dissipation.

We use the magnitude of viscous dissipation in a subducting plate as the criteria for the degree of its ``criticality''. It has been shown [6] that at a level of about 3 orders of magnitudes above chondritic heating (10^-5 W/m³), thermal instabilities are prone to occur within the lithosphere. We use that threshold value to determine in the following a critical bending moment for viscous deformation of plates.

2. Thermomechanical bending of a viscous slab We consider the deflection of a viscous plate under an external bending moment during subduction. The total bending moment M (per unit length in the x direction along the slab strike) acting on a cross section of the plate is the integrated effect of the moments exerted by the ``fiber'' stresses $\sigma_{zz}$ [5]

$\begin{displaymath} M = \int\limits_{-h/2}^{+h/2} \sigma_{zz} \, y \, dy\end{displaymath}$ (1)

on a slab with thickness h. Since we are interested only in the initial stage of deformation, we take the thin plate approximation for the fiber stresses $\sigma_{zz} = 4 \mu \dot{\epsilon}_{zz}$ with an effective viscosity $\mu$ and require, furthermore, that the strainrate $\dot{\epsilon}$ varies linearly across the slab $\dot{\epsilon}_{zz}(y,z) = \dot{\epsilon}_0 (z) \cdot 2y/h.$ After defining a `` viscous'' flexural rigidity in complete analogy to the elastic case [5,7]

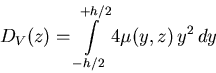$\begin{displaymath} D_V(z) = \int\limits_{-h/2}^{+h/2} 4 \mu(y,z) \, y^2 \, dy\end{displaymath}$ (2)

we obtain the momentum balance equation

$\begin{displaymath} M(z) = D_V(z) \cdot {2 \dot{\epsilon_0}(z) \over h} \quad.\end{displaymath}$ (3)

which is to be solved. Contrary to the bending equation for an elastic slab, this equation is not directly solvable but constitutes an implicit equation for the strainrate at given bending moment. This is due of the fact that the effective viscosity of slab material $\mu$ is, differently from the elastic Lamé constants, a strong function of temperature, grain-size, and stress. The viscous ``flexural rigidity'' D_V(z) therefore depends on the strainrate $\dot{\epsilon_0}(z)$ .

To solve eq. (3) numerically, we need to know the creep properties of the minerals composing the slab. We assume a pyrolitic composition and adopt the simplifying picture that the rheology is controlled by the olivine component. Once the numerical solution is obtained, the amount of dissipated energy during subduction over a distance L (slab length) per unit length in the x direction is given by

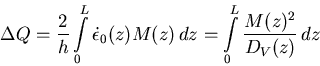$\begin{displaymath} \Delta Q = {2 \over h} \int\limits_0^L \dot{\epsilon}_0(z) M(z) \, dz = \int\limits_0^L {M(z)^2 \over D_V(z)} \, dz\end{displaymath}$ (4)

With a given temperature and flow stress at each point in the slab, one can map out its rheological structure. We use three flow-laws for which some constraints have been obtained through laboratory studies, all parameters are summarized in Table 1. In terms of these parameters, a generic flow law (i = 1, 2, 3) can be formulated

$\begin{displaymath} \dot{\epsilon} = A_i \, \Big({\sigma \over \mu_0}\Bigr)^{n_i... ...+ p V_i \over RT} (1 - {\sigma \over \sigma_{p}})^{q} \Biggr]\end{displaymath}$ (5)

where the symbols have the following meaning:
A_i: pre-exponential constant, $\sigma$ : stress, n: stress exponent, $\mu_0$ : shear modulus, b₀: length of the Burgers vector, d: average grain-size. m_i: grain-size exponent, Q_i, V_i: activation energy and volume, $\sigma_p$ : Peierls stress, q: a constant depending on the mechanism of dislocation glide [8], p: pressure, and T: temperature. Eq. (5) is used to calculate the viscosity $\mu(y,z)$ for a given surface strainrate $\dot{\epsilon_0}(z)$ for all possible creep mechanisms. We assume that all mechanisms act independently and add up together in a linear manner to yield a composite flow law, which implies that the mechanism that gives the lowest viscosity is prevailing at a local spatial point (y,z).

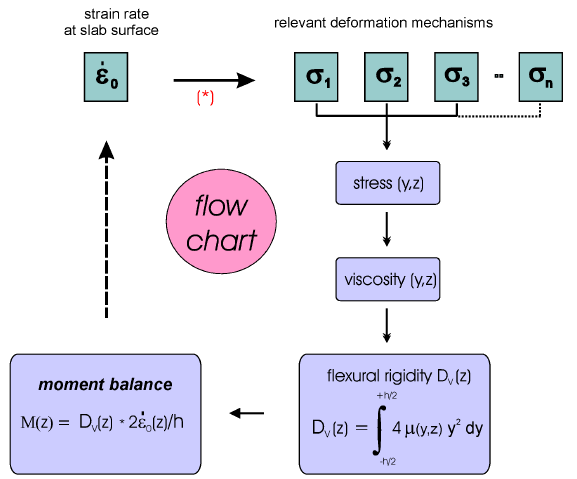
The solution of the bending moment equation enables us to calculate the stress - strain in a highly inhomogeneous slab with a typical spatial resolution of 100 meter or finer in two dimensions. We choose this discrete approach to avoid numerical problems in solving partial differential equations with high viscosity contrast and localization phenomena arising from possible non-linear feedback mechanisms of the coupled thermo-kinetic-mechanical system, as it happens when the effects of a high-pressure phase transformation were taken into account [3]). The iteration scheme used is depicted as a flow chart in Fig. 1. We note that a nonlinear feedback process is resulting from this algorithm.

3. Critical behaviour The complexity of rheology in subducting slabs due to their heterogeneous thermal and mineralogical structure gives rise to a complicated pattern of viscous flow. In this regard, a thermo-mechanically coupled slab appears to be similar to any nonlinear dynamical system that organizes itself into various stable and unstable states, depending on the so-called ``order parameter'' that controls the state of the system [9,10]. A ``critical'' system in this generalized sense is a system consisting of many nonlinearly interacting constituents but exhibits some general characterisitic behaviour in the neighbourhood of a ``critical'' value of an external control parameter. Here, for this particular problem, the viscous flexural rigidity D_V plays the role of the ``order parameter'', the independently acting creep mechanisms $\sigma_1$ , $\sigma_2$ ,.. $\sigma_n$ are the nonlinearly interacting constituents (via the order parameter D_V), and the external bending moment M is the ``control parameter''.

We find such a critical behaviour during viscous bending of a slab when M gets close to

$\begin{displaymath} M_{crit} \sim \sigma_p \cdot h^2/4 \sim 10^{19} \, \hbox{N} \quad .\end{displaymath}$

At these high bending moments, slab rheology is almost completely controlled by dislocation glide (the ``Peierls mechanism'') of olivine [11]. Eq. (1) is therefore approximated as

$\begin{displaymath} M(z) \cong 2 \int\limits_0^{h/2} \sigma_p \Bigl\{1 - \Bigl... ...epsilon}_0(z) 2 y}\Bigr]^{1 \over q} \Bigr\} \, y \, dy \quad .\end{displaymath}$ (6)

If we neglect small variations of $\sigma_p$ and Q₁+pV₁ across the slab thickness and assume for simplicity a typical geotherm along the cold center of a subducting slab according to [12]

$\begin{displaymath} T_{slab}(z) \sim 273 + T_{base} \bigl[1 - {2 \over \pi} \exp(-{\pi^2 z \over 2 Re}) \bigr] \quad ,\end{displaymath}$ (7)

with Re as the thermal Reynolds number and T_base as the lithospheric base temperature, we obtain

$\begin{displaymath} M(z) \sim \sigma_p {h^2 \over 4} \Biggl[1 - ({A_1 \over \dot... ...over q}, 2 \log({A_1 \over \dot{\epsilon}_0(z)})\Bigr) \Biggr]\end{displaymath}$ (8)

with $\Gamma(1+1/q,u)$ as the incomplete Gamma function. For large arguments u, eq. (8) can be evaluated to give [13]

$\begin{displaymath} \dot{\epsilon}_0(z) \sim A_1 \exp\Biggl[ -{Q_1+pV_1 \over RT... ... \Bigl(1-{4M(z) \over \sigma_p h^2}\Bigr)^{q} \Biggr] \quad .\end{displaymath}$ (9)

Although this relationship is still only a poor approximation of eq. (6), it shows that the strainrate at the slab surface and hence the amount of viscous heating produced by the slab material grows with a super-power law as the bending moment approaches M_crit. In addition, it shows that this instability depends only weakly on slab temperatures.

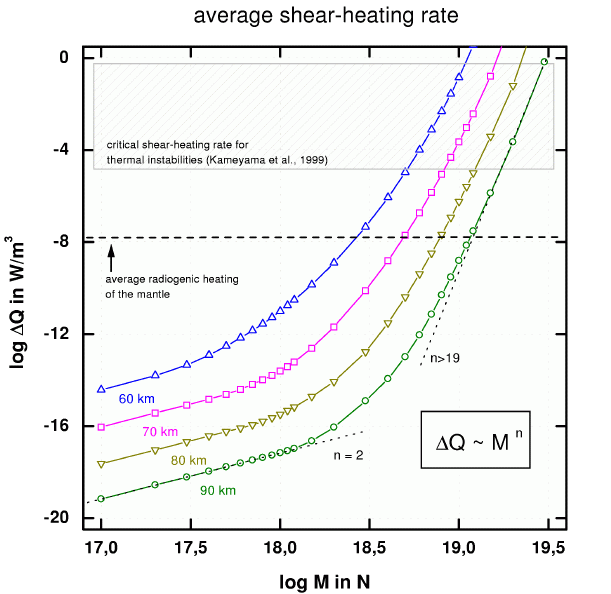
4. Numerical results The numerical solution to eqs. (2), (3), and (5) is depicted in Fig. 2. The strong divergence of viscous dissipation at a bending moment close to $M_{crit} \sim 10^{19} N$ is clearly verified, in accordance with the analytical solution (9). As a consequence, the average shear-heating rate exceeds the critical rate for the development of thermal instabilities in the lithosphere at large M-values [6], which we will use in the discussion section to define a ``critical'' range for slab bending. In the other limit, at small M-values, viscous heating scales with M² since $\dot{\epsilon} \sim M$ for linear rheology.

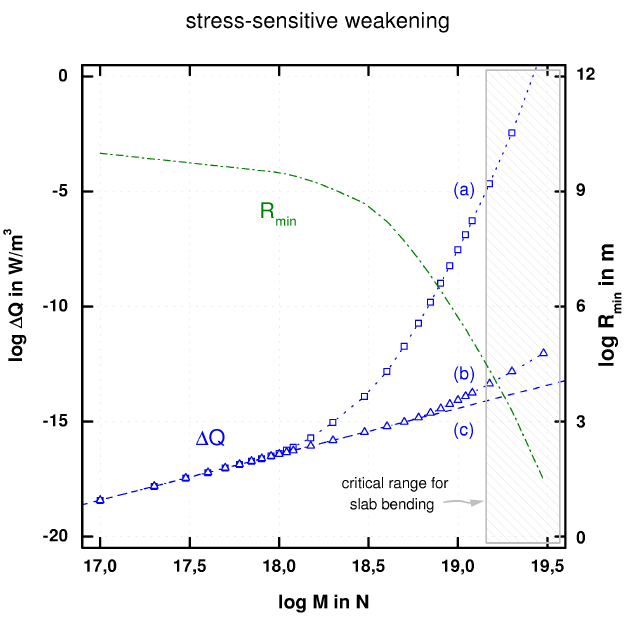
To demonstrate that this singularity indeed comes from the Peierls mechanism, we compare the numerical solution of the bending equations based on the full set of creep mechanisms (a) with the solution on the basis of a reduced set (b), where only diffusion and power-law creep are taken into account, and with a set (c) where only linear diffusion creep is contributing to slab deformation (Fig. 3). As it shows, thermal runaway is almost exclusively related to the overcoming of the Peierls barrier (plastic instability) during stress-sensitive creep.

The weakening effect on the slab caused by the high stress sensitivity of the Peierls mechanism can also be envisaged by means of a ``local'' slab curvature R(z) that may be defined according to [2] as

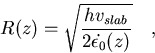$\begin{displaymath} R(z) = \sqrt{ {h v_{slab} \over {2 \dot{\epsilon_0}(z)}} } \quad ,\end{displaymath}$ (10)

where v_slab is the plate velocity. Its minimimum along the slab, R_min, defines a measure for the (local) weakness of the slab. The corresponding plot at Fig. 3 shows that for bending moments close to M_crit, slabs get highly deformable on the geological time scale, so that they loose there capability to serve as a stress guide or strong upper boundary layer in the coupled mantle - lithosphere system.

5. Discussion and conclusions Viscous heating in mantle dynamics has long been recognized as being important [14]. Yet it was not until recently [15] that this importance was demonstrated for a non-Newtonian, temperature-dependent rheology that is known to be present in the subducting lithosphere. The present approach extends this study: It includes the strong nonlinear stress dependence of the low-temperature plasticity (the Peierls mechanism) into the calculation of the viscous dissipation during subduction. The strong weakening effects from the strain-rate dependence of the slab rheology is clearly shown in Figs. 2 and 3. It is important to realize, that this stress-sensitive weakening is a consequence of the non-linear feedback mechanism inherent in the bending moment equation for viscous deformation depicted in Fig. 1: It creates a self-regulating mechanism of the coupled mantle-lithosphere system. Similar mechanisms within different contexts are responsible for the development of ``self-organized'' critical states in many physical, chemical, or biological systems [16], so that one could speculate that plate tectonics on Earth might be the result of a ``critical'' state with respect to viscous deformation.

One problem remains unsolved: Are bending moments of the order of $\sim 10^{19}$ N realistic for the Earth ? Turcotte & Schubert [5] showed that a bending moment along a plate may change considerably with depth dependent on its external loading. For example, if one side of the plate is fixed and the other side is under action of a constant force, then the bending moment varies linearly from zero at the free end to its maximum value at the fixed end.

Here, we argue that a similar situation could occur during subduction since the viscosity of the embedding mantle changes its viscosity quite significantly with depth: being largest on top of the mantle lithosphere close to the surface, getting then through a minimum at intermediate depths around 200-300 km, and getting stronger again at the bottom of the transition zone because of the pressure effect on rheology [17]. Therefore, we would expect that the bending moment for a given external force is largest at top and bottom of the slab. At the ``top'' end, where sedimentary loading [18] may play an important role, this situation usually explains why it is possible to bend slabs with extremely low viscosity [11]. At the ``lower'' end, this might be the key to understand the bending behaviour of slabs in the transition zone [3].

It is interesting to compare the situation on the other terrestrial planets and the Moon. As pointed out by Moresi & Solomatov [19], Mercury, Mars and Moon fall into the ``stagnant lid'' regime. i.e. they have very thick, strong lithospheres and convection is confined to their deep interior. To the contrary, Earth has very active surface motions and a relatively thin lithosphere within the oceanic regions. Somewhere in between is Venus which does not show plate tectonics, but may have undergone a castastrophic resurfing event about 500 Myr ago [20]. This suggests the existence of a critical threshold for driving forces in terms of a critical planetary radius. Below of that value, the driving buoyancy forces for mantle convection are not large enough to ``switch on'' plate tectonics. This observation can be understood in terms of the present results in that respect that there appears to be a sharp transition from active plate tectonics to the stagnant lid regime depending on the exerted bending moment during the initiation of subduction. Although not directly proportional, it is clear that this bending moment scales somehow with the Rayleigh number of convection, hence with the depth of the convecting layer to the third power. It is therefore appealing to speculate that there must be a critical minimum depth of mantle convection to overcome the viscous resistance forces at the upper thermal boundary layer.

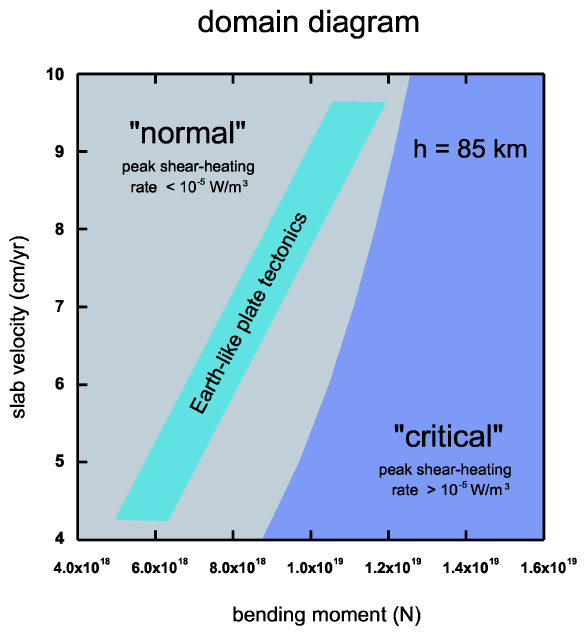
As a summary, the critical range for viscous slab bending is depicted as a domain diagram in Fig. 4 for a slab with 85 km thickness. Together with a plot of reasonable bending moments for the Earth inferred from geophysical observation [11], it shows that the transition from ``normal'' to ``critical'' behaviour of plate bending at moments in the order of 10¹⁹ Nm per m can be reached only in a few special cases with unusual tectonic settings, e.g. a thick sedimentary load of the lithosphere or a shallow angle of slab penetration at the transition zone.

Finally, we comment briefly on the possible importance of viscoelastic effects. As mentioned in the introduction, only up to 10% of the bending stresses can be supported by elastic deformation of the slab. However, this is only correct at the geological time scale. At much shorter time scales as compared with the Maxwell time, effects of elasticity may become important as well, in particular in the cold slab core, where the Maxwell time can reach values above 10⁵ years. Our analysis shows that for large bending moments close to M_crit, thermal instabilities are prone to occur within the subducted plate. Once such an instability has started, its development with time is largely controlled by the stored elastic energy [6,21].

For the investigation of the time development of such instabilities, it is essential to include the elastic component of deformation into the model. In addition, as pointed out by Schmalholz & Podladchikov [22], the pure viscous stability analysis of slab bending is limited to a low viscosity contrast between layer (slab) and matrix (mantle). A more detailed analysis of such instabilities is of particular interest with respect to a better understanding of the cause of deep focus eartquakes in the mantle transition zone.

Acknowledgements

We are grateful to Klaus Regenauer-Lieb for helpful discussions. One author (M. R. R.) wishes to thank Arie van den Berg for his hospitality during a working stay at the Institute of Earth Sciences at the University of Utrecht in May 1999.

This research has been supported by the Deutsche Forschungsgemeinschaft and the geophysics program of the National Science Foundation.

Table 1: Creep parameter for olivine

Peierls mechanism olivine [11]

pre-exponential constant A₁ 5.7 x 10¹¹ s^-1

activation energy Q₁ 540 kJ mol^-1

activation volume V₁ 1.0 x 10^-5 m³ mol^-1

Peierls stress for olivine $\sigma_{p}$ 8.5 GPa

stress exponent q₁ 2

dislocation creep olivine [23]

pre-exponential constant A₂ 3.5 x 10²² s^-1

stress exponent n₂ 3.5

activation energy Q₂ 540 kJ mol^-1

activation volume V₂ 1.0 x 10^-5 m³ mol^-1

diffusion creep olivine [23]

pre-exponential constant A₃ 8.7 x 10¹⁵ s^-1

grain-size exponent m₃ 2.5

average olivine grain-size 3 mm

stress exponent n₃ 1

activation energy Q₃ 300 kJ mol^-1

activation volume V₃ 4.0 x 10^-6 m³ mol^-1

scaling constants [8]

Burgers vector of olivine at 1 atm and 300 K b₀ 6.0 x 10^-10 m

Shear modulus of olivine at 1 atm and 300 K $\mu_0$ 81.3 GPa

FIGURES

Figure 1

Flow chart showing the numerical calculation scheme used to solve eq. (3), taking account of each contributing creep mechanism for the relevant mantle minerals. In this study, low temperature plasticity (the ``Peierls mechanism''), dislocation climb (``power law''), and diffusion creep (of ``Nabarro-Herring'' type) of olivine are considered. Because of the loop-back iteration, each of the creep mechanisms contribute nonlinearly to the viscous flexural rigidity D_V that plays the role of a mean-field ``order parameter'' of the bending process. M is the external control parameter (^(*) - input of slab temperatures, e.g. according to [12]).

Figure 2

Amount of viscous dissipation (average shear-heating rate) in a subducting slab with a thickness of 60, 70, 80, and 90 km and a subduction speed of 10 cm/yr based on the creep laws of olivine (Table 1) for an external bending moment varying between 10¹⁷ and 10¹⁹ Nm per m. At low stresses, $\Delta Q \sim M^2$ according to eq. (4) with an (almost) constant D_V.

Figure 3

Super-exponential growth of viscous dissipation $\Delta Q$ in dependence of the bending moment M for 3 different sets of constitutive equations for olivine creep (subduction speed 10 cm/yr, slab thickness 85 km):
(a) complete set including Peierls mechanism
(b) reduced set: only diffusion and power-law creep included
(c) linear rheology: only diffusion creep included
Also shown is the minimum slab bending curvature R_min in dependence of M (see text).

Figure 4

Domain diagram showing the critical range of bending moments for a slab with 85 km thickness where the lithosphere is subject to thermo-mechanical instabilities (peak shear-heating rate inside the slab larger than 10^-5 W/m³). In this ``critical'' domain, the minimum local bending curvature of the slab R_min drops down to values below the slab thickness h. Also shown is the range of plate-like tectonics on Earth as inferred from observation (cf. eg. [11]).

Next: References

Michael Riedel
7/29/1999

Peierls mechanism olivine [11]
pre-exponential constant A₁	5.7 x 10¹¹ s^-1
activation energy Q₁	540 kJ mol^-1
activation volume V₁	1.0 x 10^-5 m³ mol^-1
Peierls stress for olivine $\sigma_{p}$	8.5 GPa
stress exponent q₁	2
dislocation creep olivine [23]
pre-exponential constant A₂	3.5 x 10²² s^-1
stress exponent n₂	3.5
activation energy Q₂	540 kJ mol^-1
activation volume V₂	1.0 x 10^-5 m³ mol^-1
diffusion creep olivine [23]
pre-exponential constant A₃	8.7 x 10¹⁵ s^-1
grain-size exponent m₃	2.5
average olivine grain-size	3 mm
stress exponent n₃	1
activation energy Q₃	300 kJ mol^-1
activation volume V₃	4.0 x 10^-6 m³ mol^-1

scaling constants [8]
Burgers vector of olivine at 1 atm and 300 K b₀	6.0 x 10^-10 m
Shear modulus of olivine at 1 atm and 300 K $\mu_0$	81.3 GPa